Проект "Математика и поэзия Абая"

Калмыкова Инна,  ученица 9 «б» класса, КГУ "Глуховская средняя школа ", Восточно-Казахстанская область, Бескарагайский район,  с. Глуховка.

 

 

Руководитель: Макарова Валентина Венедиктовна, учитель математики, КГУ "Глуховская средняя школа ", Восточно-Казахстанская область, Бескарагайский район,  с. Глуховка.

 

 

Проект "Математика и поэзия Абая"

Проект "Математика и поэзия Абая"

Аннотация

В данной работе рассматриваются вопросы, связанные с применением методов математической статистики к изучению творчества великого поэта и просветителя Абая Кунанбаева. Целью проекта было выявить возможности применения математических  законов  в литературе, на примере стихосложения казахского поэта Абая. На основе методов математической статистики и анализируя законы стихосложения, автор показывает, что применив математические методы к исследованию творчества великого казахского поэта Абая (Ибрагима) Кунанбаева можно  определить принадлежность вновь найденных произведений к перу поэта и просветителя. Это исследование способствует обогащению  представления  о литературе и особенно казахской. Каждый язык имеет свою частотность применения букв и слов, что позволяет определить характерные особенности этого языка.

Аңдатпа

Бұл жұмыста ұлы ақын және ағартушы Абай Құнанбаевтың шығармашылығын зерттеуге математикалық статистика әдістерін қолдануға байланысты мәселелер қарастырылады. Жобаның мақсаты-қазақ ақыны Абайдың өлеңдерінің мысалында әдебиетте математикалық заңдарды қолдану мүмкіндігін анықтау. Математикалық статистика әдістерінің негізінде және өлең салу заңдарын талдай отырып, автор қазақтың ұлы ақыны Абай (Ибрагим) Құнанбаевтың шығармашылығын зерттеуге математикалық әдістерді қолдана отырып, жаңадан табылған шығармалардың ақын мен ағартушының қаламына жататындығын анықтауға болатынын көрсетеді. Бұл зерттеу әдебиет пен әсіресе қазақ туралы түсініктерді байытуға ықпал етеді. Әр тілдің әріптер мен сөздерді қолдану жиілігіне ие, бұл тілдің тән ерекшеліктерін анықтауға мүмкіндік береді.

Annotation

This work discusses issues related to the application of methods of mathematical statistics to the study of the work of the great poet and educator Abay Kunanbayev. The aim of the project was to identify the possibility of applying mathematical laws in the literature, on the example of the Kazakh poet Abay. It based on the methods of mathematical statistics and analyzing the laws of versification, the author shows that applying mathematical methods to the study of the work of the great Kazakh poet Abay (Ibrahim) Kunanbayev can determine the affiliation of newly found works to the pen of the poet and educator. This study contributes to the enrichment of the idea of literature and especially Kazakh. Each language has its own frequency of letters and words, which allows to determine the characteristics of the language.

Введение

40  3  05  0 100,
3  15   40:
          100  08  00  100,
    100   08  40?

 

Если просто смотреть, то перед нами набор цифр или чисел. А попробуйте с выражением прочесть. Ничего не напоминает?...

А вот отрывок из стихотворения «Что такое хорошо и что такое плохо» Владимира Маяковского

Крошка сын
к отцу пришел,
и спросила кроха:
— Что такое
хорошо
и что такое
плохо? —

 

Интересно?.. В одном случае числа, в другом слова, а звучат одинаково. И нам захотелось узнать, как связаны  математика и поэзия между собой.

Известны связи математики  с физикой, химией, биологией, черчением, а вот к литературе, кажется,  сложно найти точки соприкосновения.

Требования  современного мира к человеку возрастают в связи с увеличением информации.   Наш Президент Н.А.Назарбаев в  Послании народу сказал: «Образование должно давать не только знание, но и умение их использовать в процессе социальной адаптации…»  [9]

Вот и получается, что можно узнать, как математические законы можно применить в литературе. И я выбрала конкретное направление литературы - поэзию. Само слово «стих» в словаре Фасмера Макса :  «родительного падежа, древне-русского  стихъ, старо-славянского стихъ ,στίχος. Заимствовано из греческого  στίχος "ряд, строка, стих"».[8 ] 

Как известно понятие «ряды» изучается в математическом анализе, что подтверждает моё предположение о связи математики и поэзии.

Перед  началом проведения исследования, я выдвинула гипотезу: математические методы помогают  поэтам писать самобытные и красивые стихи, устанавливать авторство неизвестных произведений.

Я поставила  себе цель: выявить возможности применения математических  законов  в  стихосложении и особенно в творчестве Абая, познакомиться с практическим применение методов математической статистики.

В соответствии с этим определили  задачи: 

•   Определить связь между математикой и поэзией;
•  Оценить влияние математических законов на поэзию;
•  Рассмотреть возможность применения статистических методов для  определения авторства работ;
• Исследовать некоторые  произведения  Абая с точки зрения математики.  

Объектом исследования мы выбрали  поэзию, творчество казахского поэта Абая, который родился в Чингисских горах Семипалатинской области в кочевьях рода Тобыкты, известен всему миру.

Предмет исследования – это стихосложение,  лексика, законы математики в произведениях поэтов, методы математической статистики.

Известный немецкий математик XIX века Г. Вейль произнес слова: "Занятия математикой сродни мифотворчеству, литературе или музыке. Это одна из наиболее присущих человеку областей его деятельности, в которой выражается его человеческая сущность, стремление к интеллектуальной сфере жизни, выступающей одним из проявлений мировой гармонии". [ 6 ]

Именно гармония  является объединением математики и литературы.

МАТЕМАТИКА И ПОЭЗИЯ

В начале было слово.

«Математики как французы: все, что вы им говорите, они переводят на свой язык, и это тотчас же становится чем то совершенно иным.»

Иоганн Вольфганг Гёте

Первое исследование я провела, изучая одинаковые слова в математике и литературе. Результат  оформила в таблицу 1.

ТАБЛИЦА 1

Слово	В литературе	В математике
Произведение	Произведение  в литературе –это результат работы писателя.	Произведение в математике – это  результат умножения.
Инверсия  (лат. inversio — переворачивание, перестановка)	Инверсия в поэзии — нарушение порядка ударений в стихе. Словесное ударение находится не на ожидаемом месте стиха, а падает на соседний слог (слоги оказываются "переставленными", инвертированными). Пушкин считал инверсию одной из главных фигур поэтической речи, причем нередко поэт использовал не только контактную, но и дистанционную инверсию, когда при перестановке слов между ними вклиниваются другие слова: «Покорный Перуну старик одному…».	Инверсия (логика), отрицание — переворачивание смысла, замена «белого» «чёрным». Инверсия (геометрия) — конформное преобразование евклидовой плоскости или пространства. Инверсия (перестановка) — термин, относящийся к перестановкам в математике; либо пара ключей, которые нарушают порядок в файле[1]. Инвертирование (компьютерные науки) — битовая операция, переводящая 0 в 1 и 1 в 0. Логическое НЕ.
Антипод греческого происхождения происходит от анти - противопоставление, не, и греч. поус - нога, стопа antithesis  противопоставление .	Антипод - это противопоставление, термин используется в теории литературы для обозначения полной противоположности характера одного персонажа другому. Например, в произведении Гончарова "Обломов" деятельный и активный Штольц является антиподом ленивого и пассивного Обломова, хандрящий и уставший от жизни Евгений Онегин является антиподом Владимира Ленского - романтика и поэта, который верит в силу любви.	Антипод - это точка на земной поверхности диаметрально противоположна данной точке, Например Северный полюс это антипод Южного полиса. В другом значении Антипод - это любое противоположное явление или предмет. Противоположные числа
Фигуры	Латинское слово «фигура» имеет много значений, одно из которых напрямую связано с поэзией. В стихотворных произведениях фигура появляется под влиянием сильных переживаний, которые автор хочет сообщить читателю. В этом случае он несколько отступает от выбранного стиля изложения, благодаря чему участок текста, где используется фигура, выделяется не только сильной эмоциональностью, но и иным структурным построением.	Плоская фигура — связное замкнутое подмножество , ограниченное конечным числом попарно не пересекающихся жордановых кривых.   В случае, если все входящие в состав границы плоской фигуры кривые являются ломаными, то фигура называется многоугольной фигурой. Односвязная многоугольная фигура является многоугольником.
Гипербола из древнегреческого: «переход; чрезмерность, избыток ...»	Гипербола в литературе это художественный приём, который заключается в намеренном преувеличении масштабов явления с целью придания фразе большей выразительности и эмоционального накала. Примеры:  «я тебе 100500 раз уже об этом говорил!»  «у нас ещё патронов вагон и маленькая тележка, прорвёмся!»  «мне до вашего сердца, мадам, как до Луны пешком!»	Гипербола в алгебре это кривая графика функции обратной пропорциональности. Гипербола в геометрии это кривая, образованная сечением конуса плоскостью. Гипербола похожа на параболу, но отличается от неё формальным определением.
Сравнение	СРАВНЕНИЕ - это художественный прием (троп), при котором образ создается посредством сравнения одного объекта с другим. Сравнение отличается от других художественных сопоставлений, например, уподоблений, тем, что всегда имеет строгий формальный признак: сравнительную конструкцию или оборот со сравнительными союзами как, будто, словно, точно, как будто и подобными. Выражения типа он был похож на…нельзя считать сравнением в качестве тропа.	эмпирическая процедура, устанавливающая тождество (сходство) или различие исследуемых пар объектов, явлений и т. п. С принципиальной точки зрения (в общеметодологическом плане) сравнивать между собой можно любые мысленные объекты, но при условии, что сравнение производится по какому-либо точно выделенному в них признаку, свойству, отношению, т. е. в рамках заданного интервала абстракции. Ф.В. Лазарев В математике термин «сравнение» переплетается с аналогичным понятием «отношение». Сравнивая числа на равенство либо неравенство, мы находим разницу между ними(больше-меньше). ... . -
Усиление (возрастание)	Усиление или градацияПри использовании этого выразительного средства автор располагает тезисы, аргументы свои мысли и т.д. по мере увеличения их важности или убедительности. Подобное последовательное изложение позволяет многократно увеличить значимость излагаемой поэтом мысли.	Функцию у = f(x) называют возрастающей на промежутке, если для любых x1 и x2 принадлежавших этому промежутку, из условия x2 > x1 следует, что f(x2) > f(x1). Т.е. положительному приращению аргумента ∆х = x2 − x1 >0 соответствует положительное приращение функции ∆f = f(x2) − f(x1) > 0.

 

Можно увидеть, многие термины встречаются как в математике, так и в литературе: гипербола, парабола, метр, параллелизм… Да  и результат работы писателя в литературе  и результат умножения в математике называется одинаково - произведение.

Что даёт нам  это совпадение? О чём оно говорит?

Поиски  ответов  на эти вопросы  привели меня  к такой науке как «Математическая лингвистика».  Математическая лингвистика  занимается изучением возможностей применения математических методов к научному описанию языков.

Основателем математического описания языка считают известного швейцарского лингвиста Фердинанда де Соссюра. В 50-х годах 20 –го столетия Соссюр выделил слово как  «знак», в котором соединились звучание и смысл.

Как известно математика помогает изучать явления и процессы, создавая математические модели. Использование математических приемов при систематизации, измерении и обобщении лингвистического материала позволяет языковедам глубже проникнуть в тайны построения языка и образования текста.

Для описания и исследования лингвистических фактов привлекаются различные разделы математики: алгебра, теория множеств, математическая логика, теория информации, теория вероятностей и математическая статистика. В силу этого математическая лингвистика стала развиваться в нескольких направлениях - алгебраическая лингвистика, комбинаторная лингвистика, которая опирается на разделы «неколичественной» математики (теория множеств, математическая логика, теория алгоритмов), и квантитативная лингвистика, которая изучает лингвистические явления с помощью «количественной математики» (математическая статистика, теория вероятностей, теория информации и др.)

Лингвистическое измерение математики сводится к рассмотрению математического языка. Физик Н. Бор писал: «Мы не будем рассматривать чистую математику как отдельную область знания; мы будем считать ее скорее усовершенствованием общего языка…».  Подобно любому языку язык математики состоит из совокупности высказываний (предложений),  в нем широко используются математические символы, объединяемые формулой. Впрочем, в  любом математическом труде используются такие слова и обороты , заимствованные из естественных языков: «предположим, что…», «и будем исходить из следующих аксиом» и т.п. Но в контексте математики этим словам и оборотам речи придается специфическое значение, которое сопрягается со смыслом формализованных утверждений.

И так получается, что математическая лингвистика является связующим звеном математики и литературы, ведь  литература  как основу  использует язык.

Как известно в 60-70-ых  годах  20 века развиваются и компьютерные технологии. В то время их пытались применить к переводам с одного языка на другой.  Вот толкования определения «математической лингвистики» из толкового словаря:

Математическая лингвистика:

1. Изучает особенности семиотического и математического моделирования естественного языка (и речи) с целью перевода информации, содержащейся в неформализованном виде в тексте, на формализованный искусственный язык (например, на некоторый информационный язык) на основе такого математического аппарата, как теория множеств и алгебра отношений, теория нечетких множеств и лингвистической переменной, теория вероятностей и математическая статистика, а так же элементов теории информации. Тесно связана с инженерной лингвистикой.

Однако первое поколение систем машинного перевода было весьма несовершенным. Все они базировались на алгоритмах последовательного перевода «слово за словом», «фраза за фразой» – смысловые связи между словами и предложениями никак не учитывались.

Учёные задумались над тем, как нужно формализовать и строить алгоритмы для работы с текстами, какие словари надо вводить в машину, какие лингвистические закономерности следует использовать при машинном переводе. Ни для одного языка в то время не существовало перечней синтаксических конструкций, не были изучены условия их сочетаемости и взаимозмаеняемости, не были разработаны правила построения крупных единиц синтаксической структуры из более мелких составляющих элементов.

Потребность в создании теоретических основ машинного перевода и привела к формированию и развитию математической лингвистики. Ведущую роль в этом деле в СССР сыграли математики А.А. Ляпунов, О.С. Кулагина, В.А. Успенский, лингвисты В.Ю. Розенцвейг, П.С. Кузнецов, Р.М. Фрумкина, А.А. Реформатский, И.А. Мельчук, В.В. Иванов. 

В наше время появляются новые технологии машинного перевода, основанные на использовании систем искусственного интеллекта, статистических методах. [17]

Напомню, что математическая статистика – это наука, занимающаяся методами обработки экспериментальных данных.

Статистика является одной из древнейших отраслей знаний, возникшей на  базе  хозяйственного  учета.  Предполагают,  что  термин «статистика»  произошел  либо  от  латинского  слова «status» (статус), что  означает «порядок», «состояние и положение дел/вещей», либо от слова «stato» (стато), что означает «государство». Статистика занимается изучением количественной стороны массовых общественных явлений и процессов в числовой форме, выявляя особые закономерности.

 Из учебников я узнала основные характеристики и формулы статистики.

Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.

Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.

Одно из главных направлений статистики – надлежащая обработка информации. Статистические исследования над большим количеством литературных текстов показали, что частоты появления той или иной буквы (или пробела между словами) стремятся при увеличении объёма текста к некоторым определённым константам. Таблицы, в которых собраны буквы того или иного языка и соответствующие константы, называют частотными таблицами языка.

Частотность — термин лексикостатистики, предназначенный для определения наиболее употребительных слов. Расчёт осуществляется по формуле:{\displaystyle Freq_{x}={\frac {Q_{x}}{Q_{all}}},}

где  F_reqx — частотность слова «x»,  Q_x — количество  словоупотреблений 

слова «x», Q_all — общее количество словоупотреблений. В большинстве случаев частотность выражается в процентах. В словарях частотность слов может отражаться пометками - употребительное, малоупотребительное и т. д.

Аналогичным образом определяется частотность для букв. Бо́льшая частотность согласных на данном отрезке текста (например, в стихотворениях) получила название аллитерации. Высокие показатели частотности гласных называются ассонансом.

Частотный анализ предполагает, что частота появления заданной буквы алфавита в достаточно длинных текстах одна и та же для разных текстов одного языка. Частотный анализ используется в криптографии для выявления наиболее частотных букв того или иного языка. [ 8 ]

Частотные таблицы языка – это таблицы, в которых собраны буквы того или иного языка и соответствующие им константы.

Русский алфавит кириллический. За время своего существования он пережил несколько реформ, в результате которых сложилась современная русская азбучная система, включающая 33 буквы.

Частотная таблица русского языка:

1	О	9,28 %	12	П	3,35 %	23	Ч	1,27 %
2	А	8,66 %	13	М	3,29 %	24	Ю	1,03 %
3	Е	8,10 %	14	У	2,90 %	25	Х	0,92 %
4	И	7,45 %	15	Д	2,56 %	26	Ж	0,78 %
5	Н	6,35 %	16	Я	2,22 %	27	Ш	0,77 %
6	Т	6,30 %	17	Ы	2,11 %	28	Ц	0,52 %
7	Р	5,53 %	18	Ь	1,90 %	29	Щ	0,49 %
8	С	5,45 %	19	З	1,81 %	30	Ф	0,40 %
9	Л	4,32 %	20	Б	1,51 %	31	Э	0,17 %
10	В	4,19 %	21	Г	1,41 %	32	Ъ	0,04 %
11	К	3,47 %	22	Й	1,31 %	33	Ё	0,04 %

Статистика частотности букв русского языка (на материале НКРЯ):

Частотность букв  русского языка показала, что чаще всего используются гласные буквы «о», «е», «а», «и», из соглассных «н», «т», «с», «в». Редко встречаются «ъ» и «ё».

Частота встречаемости букв в английском языке.

Как известно, самая часто встречаемая буква - E, редко встречаемая - Z.
Вот наглядная таблица английского алфавита

Буква	a	b	c	d	e	f	g	h	i	j
частота	8,17	1,49	2,78	4,25	12,70	2,23	2,02	6,09	6,97	0,15
Буква	k	l	m	n	o	p	q	r	s	t
частота	0,77	4,03	2,41	6,75	7,51	1,93	0,10	5,99	6,33	9,06
Буква	u	v	w	x	y	z
частота	2,76	0,98	2,36	0,15	1,97	0,07

 

Частотных таблиц  букв казахского языка я не нашла поскольку они  находятся в разработке. К тому же история казахского языка богата, до революции использовалась арабская вязь, с 1929 по 1939 год латиница, в 1940 году  перешли к кириллице, сейчас готовится  переход к латинице.

Казахский алфавит (основанный на кириллице) содержит 42 буквы.

Я взяла  текст Мухара Әуезова  (т. 2стр. 180) и попробовала подсчитать частоту использования букв. Всего в выбранном тексте 1313 знаков, подсчёты частоты и относительной частоты я оформила в таблицу 2. 

ТАБЛИЦА 2

№	Буква	частота	относительная частота	№	Буква	частота	относительная частота
1.	а	123	0,0937	22	п	23	0,0175
2.	ә	22	0,0168	23	р	76	0,0579
3.	б	33	0,0251	24	с	69	0,0526
4.	в	4	0,0030	25	т	50	0,0380
5.	г	7	0,0053	26	у	24	0,0183
6.	ғ	17	0,0129	27	ұ	24	0,0183
7.	д	47	0,0358	28	ү	13	0,0099
8.	е	103	0,0784	29	ф	0	0
9.	ё	0	0	30	х	3	0,0023
10	ж	31	0,0236	31	һ	0	0
11	з	44	0,0335	32	ц	0	0
12	и	5	0,0038	33	ч	0	0
13	й	35	0,0267	34	ш	15	0,0114
14	к	21	0,0160	35	щ	0	0
15	қ	43	0,0327	36	ъ	0	0
16	л	58	0,0442	37	ы	103	0,0784
17	м	37	0,0282	38	і	112	0,0853
18	н	96	0,0731	39	ь	0	0
19	ң	2	0,0015	40	э	0	0
20	о	43	0,0327	41	ю	0	0
21	ө	29	0,0220	42	я	1	0,0008

 

Лидируют среди гласных буквы а, і, ы, е, среди согласных –н,р,с,л.  Ориентировочные значения частот отдельных букв казахского языка на основе одной из статей о музыке  на казахском языке я взяла из исследований Кажикенова С.Ш., Мазиева К. Текст содержит знаков с пробелами –500, без пробелов –431 результаты представлены в таблице 3 (тире здесь обозначает пробел между словами). Из таблицы 3 видно, что чаще всего встречаются гласные – ы, а, согласные – р, м. некоторые буквы в данном тексте отсутствуют.

 

ТАБЛИЦА 3

буква относ.частота	__ 0,138	ы 0,124	а 0,112	р 0,052	м 0,05	н 0,044	е 0,042	т 0,042
буква относ.частота	к 0,036	л 0,036	д 0,034	і 0,032	з 0,028	ң 0,026	с 0,026	у 0,022
буква относ.частота	б 0,018	й 0,018	қ 0,018	ж 0,014	о 0,014	ә 0,01	ө 0,01	х 0,01
буква относ.частота	ғ 0,008	п 0,008	ү 0,008	ш 0,006	г 0,004	и 0,004	я 0,004	ұ 0,002

Существуют множество различных таблиц о распределении букв в том или ином языке, но ни одна из них не содержит окончательной информации - даже порядок букв может отличаться в различных таблицах. Распределение букв очень сильно зависит от типа теста: проза, разговорный язык, технический язык и т.п.

О красоте и богатстве языка принято судить по количеству слов, которые отображены в словаре. Это один из показателей культурного развития нации. Этот аспект важен при изучении и овладении языком.  Для создания частотных словарей – словарей, в которых приводятся числовые характеристики употребительности слов (словоформ, словосочетаний) какого-либо языка – языка писателя, какого-либо произведения и т. п. используются статистические закономерности в языке.

По данным The Global Language Monitor, самый богатый словарный запас у англичан — более 1 млн слов. Следом идет китайский язык (более 500 тысяч), японский (232 тысячи), испанский богат 225 тысячами слов.

По поводу слов ещё хочется отметить, что по заблуждению некоторых людей запас казахского языка довольно скудный.

«Поистине: невежество — бич разума.
Я всегда испытываю стыд и неловкость оттого, что иные казахи, по тем или иным причинам давно отлученные от этнических корней, от родного языка, с апломбом говорят о его скудности.» [ 5 ]

СПРАВКА

Мухтар Ауэзов только в «Пути Абая» использовал 16 893 слова. В самом большом словаре - академическом 17-томном «Словаре современного русского литературного языка» - зарегистрировано и объяснено 120 тысяч 488 слов. В 1953 году, когда  готовили к изданию первый однотомник казахского толкового словаря, в фонде (картотеке) Академии наук Казахской ССР насчитывалось 180 тысяч слов, а уже в 1972 году эта картотека состояла из 2 миллионов 550 тысяч слов. [ 5 ]

Лингвистика — неточная наука. Хотя бы потому, что филологи так и не договорились, как различать слова и словоизмененные формы. Поэтому, чтобы достичь точности в определении, в каком языке больше слов, необходимо исследовать словари:

«Большой казахско-русский/русско-казахский словарь»

(под общей ред. К. Бектаева) содержит 85 тысяч слов;

«Словарь казахского литературного языка» (15 томов, 2011) показывает 150 тысяч единиц;

«Толковый словарь казахского языка» (2013) — 106 тысяч слов и 48,3 тысячи словосочетаний.

Так что те, кто верит в 2,5 млн или 200 тысяч слов, обманываются.

Академия наук Казахской ССР в начале 1950-х годов готовила издание толкового словаря казахского языка. Сотрудники собрали материал (создали картотеку), который отображал лексические единицы, употребляемые в литературном контексте.

Всего таких записей (карточек) было 2 млн 550 тысяч. В них были представлены слова казахского языка, употребленные с разными значениями в разных контекстах. Спутывание количества единиц языка и форм их отображения привело к рождению этого мифа. [18 ]

Применение статистических методов к исследованию стихов Абая.

«..человека, умеющего наблюдать и анализировать, обмануть просто невозможно. Его выводы будут безошибочны, как теорема Евклида.» 
Артур Конан Дойль

 

  Одной из задач статистики является задача проверки правдоподобия гипотез. Она может быть сформулирована следующим образом: имеется совокупность опытных данных, относящихся к одной или нескольким случайным величинам.

И действительно, мы привыкли к тому, что литература – это всегда чтение текстов и их анализ. А что если взять очень много разных текстов и представить их с количественной точки зрения?

У каждого автора есть своя частотная таблица использования букв, слов, специфических литературных оборотов и т. п. По этой частотной таблице можно определить автора текста примерно так же, как по отпечаткам пальцев. Например частотная таблица, А.С. Пушкина.

 

Частотная таблица А.С.Пушкина:

О	8,3 %		М	2,8 %		[ ]	1,7 %
Е	7,1 %		К	2,4 %		Ч	1,1 %
А	6,1 %		У	2,4 %		Ж	0,09 %
Н	5,9 %		П	2,1 %		Ф	0,08 %
И	5,2 %		Ы	1,9 %		Х	0,08 %
Т	4,7 %		Б	1,4 %		Э	0,07 %
Л	4,3 %		З	1,4 %		Ш	0,06 %
С	4,2 %		Г	1,5 %		Ю	0,06 %
В	3,7 %		Я	1,6 %		Ц	0,03 %
Р	3,7 %		Ь	1,7 %		Ъ	0,02 %
Д	2,9 %		Й	1,8 %		Щ	0,01 %

Частотных таблиц казахских писателей мало и найти их сложно. Я  провела статистическое  исследование на примере произведений Абая. Великий казахский поэт-просветитель Абай Кунанбаев создал около 170 стихов, 56 переводов, написаны поэмы, а в конце жизни появились «Слова назидания» -  «Қара сөздер».Я рассмотрела несколько стихов и  составила частотную таблицу языка Абая. Всего  в выборке 1944 знака.

Частотная таблица И. Кунанбаева.

№	Буква	частота	Относит частота	№	Буква	частота	Относит  частота
1.	а	142	0,0730	22	п	69	0,0355
2.	ә	13	0,0067	23	р	75	0,0386
3.	б	80	0,0412	24	с	113	0,0581
4.	в	0	0	25	т	142	0,0730
5.	г	28	0,0144	26	у	8	0,0041
6.	ғ	23	0,0118	27	ұ	6	0,0031
7.	д	80	0,0412	28	ү	27	0,0139
8.	е	222	0,1142	29	ф	0	0
9.	ё	0	0	30	х	16	0,0082
10	ж	69	0,0355	31	һ	0	0
11	з	26	0,0134	32	ц	0	0
12	и	5	0,0026	33	ч	0	0
13	й	50	0.0257	34	ш	25	0,0129
14	к	44	0,0226	35	щ	0	0
15	қ	41	0,0211	36	ъ	0	0
16	л	98	0,0504	37	ы	78	0,0401
17	м	90	0,0463	38	і	136	0,0700
18	н	105	0,0540	39	ь	0	0
19	ң	52	0,0267	40	э	0	0
20	о	45	0,0231	41	ю	0	0
21	ө	33	0,0170	42	я	3	0.0015

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В афавите 15 гласных и общая  сумма их частот 718, а отношение, показывающее среднее арифметическое  718/15= 47,87,  26 согласных и сумма их частот 1226, среднее  арифметическое 1226/26= 47,15. Это показывает, что гласные используются Абаем чаще чем согласные, этим можно объяснить певучесть его стихов.

Для выявления особенностей стиля, и языка автора рассмотрим   некоторые характеристики количественного распределения слов в поэзии Абая Кунанбаева и приведём  сравнение этих характеристик для собственного творчества Абая и его переводов стихов русских классиков.

Расшифровка произведений с точки зрения их авторства имеет чрезвычайно большое значение для правильной оценки культурного наследия нации. Это значение определяется необходимостью изучения определенной литературной эпохи, историей общественно - революционного движения, особенностями процессов литературной борьбы, а также историей литературных изданий и эволюцией формирования крупных художников слова.

Выдвинута гипотеза о том, что частая встречаемость слов в тексте определённой длины отражает языковую связь этих слов, и позволяет распределить тексты  по стилям.  Воспользуемся выборочным исследованием. В статистическую совокупность стихотворений Абая, по которой я наблюдала свойства лексики, включено 26 произвольно избранных стихотворений, из них 12 являются его собственными произведениями, 14 — переводные стихотворения ПушкинаА.С, Лермонтова М.Ю., Крылова И.С., Я. Полонского. Общее количество слов (длина обследованного текста) составляет 4152, в том числе: 1988 слов относится к тексту собственного творчества и 2164 — к переводам. Совокупность в 26 стихотворениях содержит 1345 различных слов. Подгруппа стихов собственного творчества написана при помощи 861 слов и подгруппа переводных — 813 слов.

 В таблице 4 представлен список 70 слов наибольшей частоты в совокупности стихотворений Абая. Сюда включены слова, частота которых от 82 до 11 рассчитана для обеих подгрупп совместно.

 

слово	Стихи в совокупн.				в скольких Стихах в совокупн			место
	всего	собств.		Перев.		В собств.	В Перев.	Среди собств.	Среди Перев.
деу	82	60		22	19	10	9	1	10,5
болу	76	30		46	21	10	11	5	2
бір	72	31		41	21	10	11	4	3
мен (я)	68	15		53	14	6	8	15	1
да, де,…	62	33		28	18	8	10	2	7,5
өз	53	17		36	20	9	11	12	14
алұ	53	22		31	19	6	13	7	6
сен	48	14		34	13	6	7	17,5	5
сөз	46	32		14	16	7	9	3	21
жоқ	41	19		22	15	7	8	9	10,5
көру	41	19		22	13	5	8	9	10,5
ол	37	17		20	16	7	9	12	13,5
е (быть)	35	7		28	13	14	9	48	7,5
келу	33	14		19	17	7	10	17,5	15
кылу	33	17		16	17	10	7	12	17
беру	33	23		10	13	6	7	6	35
бар	31	9		22	11	4	7	40	10,5
не	27	7		20	11	5	6	48	13,5
түру	25	7		18	12	5	7	48	16
ма, ме,...	25	11		14	11	6	5	27,5	21
журу	25	19		6	9	5	4	9	56
жак (душа)	24	11		13	14	6	8	27,5	24,5
білу	24	9		15	12	5	7	41	18,5
жұрт	24	15		9	12	6	6	15	38,5
жүрек	24	12		12	11	6	5	23	28
айту	24	11		13	10	3	7	27,5	24,5
көту	22	8		14	15	7	8	45	21
шыгу	22	10		12	13	5	8	34	28
іс	22	11		11	10	6	4	27,5	31,5
көп	21	13		8	13	8	5	20	44
сол (тот)	21	15		6	13	9	4	15	56
бас	21	10		11	12	5	7	34	3,5
бәрі	20	9		11	12	6	6	41	31,5
көңіл	20	12		8	12	6	6	23	44
күн	20	10		10	11	6	5	34	35
үшін	19	10		9	11	6	5	34	38,5
жас (молодой)	19	4		15	8	3	5	63	18,5
салу	18	5		13	12	4	8	56,5	24,5
бұл	18	10		8	10	6	4	33	44
жер	18	10		8	10	6	4	33	14
дос	17	10		7	12	6	6	34	50
айла	17	12		5	5	2	3	23	61,5
сорлы	16	4		12	9	3	6	63	28
ойлау	16	3		13	9	3	6	68,5	24,5
мән (с)	16	13		3	7	5	2	20	67
табу	15	9		6	10	5	5	41	56
өлу	15	5		10	7	2	5	56,5	35
өту	14	3		11	8	3	5	68,5	31,5
ел	14	13		1	7	6	1	20	68,5
қалу	13	4		9	9	2	7	63	38,5
тіл	13	9		4	9	6	3	42	65
осы	13	6		7	7	2	5	52	50
үй	13	9		4	5	3	2	41	65
қарау	12	4	8		9	3	6	63	44
бой	12	4	8		9	3	6	63	44
қайғы	12	3	9		8	3	5	68,5	38,5
кісі	12	11	1		7	6	1	27,5	68,5
қызық	12	5	7		7	2	5	56,5	50
кім	12	7	5		6	2	4	48	61,5
адам	11	6	5		9	5	4	52	61,5
біреу	11	7	4		8	4	4	48	65
дүние	11	5	6		8	4	4	56,5	56
қою	11	6	5		8	4	4	52	61,5
жүз (лицо)	11	5	6		8	4	4	56,5	56
іш	11	4	7		7	3	4	63	50
жату	11	5	6		7	3	4	56,5	56
ер	11	3	8		6	3	3	68,5	44
жар (супруг)	11	4	7		5	1	4	63	50
мал	11	11	0		4	4	0	27,5	70

 

Я показала как статистические методы позволяют построить математическую модель языка, что может оказать помощь  для его изучения. Ведь предполагается, что художественная литература на иностранном языке даёт богатейший языковой материал, который тесно соприкасается с общеупотребительным словарем разговорного языка, что позволяет обогатить лексический запас и  помогает в изучении языка.

 Напомню, что математические модели рассматривались как инструмент  для работы с текстами, чтобы выяснить, какие лингвистические закономерности следует использовать при определении авторства, они применимы и в  машинном переводе. Системы машинного перевода позволили создать автоматические обучающие системы,  ведь количественные данные часто помогают более глубоко осмыслить изучаемые явления. Ответ на вопрос «сколько» помогает ответить и на вопросы «что», «как», «почему»  в этом особенность количественной характеристики. 

Выявление частотности слов широко распространено в автороведческой экспертизе, осуществляемой на основе последовательного применения количественных методов. Так, в качестве признаков стали использоваться слова, сгруппированные по частоте встречаемости в тексте. Наиболее типичными для текста являются группы слов, встретившиеся в нем один(hapax legomena) или два раза(dis legomena), – такие слова, как правило, преобладают в большинстве текстов, и чаще всего это знаменательные слова. Например, мерой  К, учитывающей описанное выше распределение, являет-ся оценка, предложенная Юлом(G.U. Yule).

Расчет величин характеристики Юла для каждого стихотворения в отдельности (входящего в нашу совокупность) мы производили по формуле: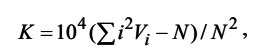

Где Vi– количество слов, встретившихся в тексте i раз, N– количество слов в  тексте. Оценку K можно интерпретировать как коэффициент повторения слова в тексте: чем чаще повторяется произвольно выбранное слово, тем выше коэффициент K. Соответственно, чем выше значение K, тем беднее словарь автора.  

В таблице 5 приведены величины К для отдельных стихов нашей совокупности стихотворений Абая.

Объём совокупности n= 1345 различных слов, выборки- n₁=1988 слов  из собственных сочинений, n₂=2164 слова из переводов.

	Размах  К	Медиана  К
Собственные произведения	213,16	60,945
Переводы	210,81	71,27

 

 

 

ТАБЛИЦА 5

Величины характеристики К избранных стихотворений Абая с указанием автора оригинала и переводов

Стихотворение (том, стр.)	К	Автор		Стихотворение (том, стр.)	К	Автор
I       62	23,13	-		I     112	69,91	Пушкин А.С.
II     106	24,63	-		II      78	70,00	Крылов И.С.
I       203	25,68	-		II      68	72,54	Крылов И.С.
I      173	32,25	Лермонтов М.Ю.		I      185	73,61	Лермонтов М.Ю.
II       59	44,44	-		II      33	75,95	Лермонтов М.Ю.
I      107	46,00	Лермонтов М.Ю.		II      81	80,62	-
	52,54	Лермонтов М.Ю.		I      117	83,28	Пушкин А.С.
	54,00	Лермонтов М.Ю.		II     109	83,67	-
	55,39	Лермонтов М.Ю.		II      94	86,00	Полонский Я.
I        55	59,67	-		I       115	98,03	Пушкин А.С.
II       91	61,02	-		I       17	149,52	-
I        47	61,55	-		I      123	236,29	-
I        49	60,87	-		I        14	243,06	Лермонтов М.Ю.

 

 Для совокупности среднее значение К  равняется     77,832;

 для подгруппы стихов собственного творчества — 75,92

                                                  для переводов —       79,46.

Указанные величины показывают, что повторяемость слов в переводах немного превышает повторяемость в стихах собственного творчества.

Изучить зависимость распределения лексических единиц от содержания позволяют только свойства подгруппы переводных стихов.

 Приведем снова величины К для переводов, на этот раз отдельно по авторам оригиналов, с указанием средней К для отдельного автора и соответствующих величин дисперсии, рассчитанной по формуле:

         ,

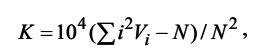где i обозначает стихотворение  надлежащего автора,  n – число стихотворений.

ТАБЛИЦА 6

Величины К переводов, на этот раз отдельно по авторам

оригиналов и соответствующих величин дисперсии

 

Пушкин А.С.	83,28	= 76,65	S2  = 249,62
	98,03
	69,91
	55,39
Крылов И.С.	72,52	=65,51	S2 =67,35
	70,00
	54,00
Лермонтов М.Ю.	32,65	= 56,09	S2 = 276,83
	46,00
	52,54
	73,61
	75,95

 

 Изменчивость величин  К  у отдельного автора измеряется дисперсией. Наименьшая дисперсия величины К наблюдается в стихотворениях Крылова И.С. Напротив, переводы из творчества Пушкина А.С и Лермонтова М.Ю. имеют примерно одинаковую величину S². Это явление можно объяснить следующим образом: стихи Лермонтова М.Ю., так же как и отрывки из «Евгения Онегина» Пушкина А.С., носят выразительно лирический характер. Басни Крылова И.С. представляют эпический жанр. Учитывая это, можно прийти к заключению, что величина  К в эпических произведениях имеет большую изменчивость, чем в лирике. Если присоединим к басням Крылова И.С. собственную басню Абая «Есек» (т. 2, стр. 84), где K=80,62, то вновь образовавшаяся прогрессия величин К получит S²=93,31. И эта величина резко отличается от дисперсии в переводных стихах Лермонтова М.Ю. и Пушкина А.С.. В остальных стихах собственного творчества Абая явна большая изменчивость. Следовательно, можно сделать вывод, что эпические стихи по свойству распределения лексических единиц носят более близкий характер, чем стихи лирические.

 Учитывая, что в изучаемый нами набор входят отдельные стихотворения, и имея в виду подразделение их на две подгруппы, эпические и лирические, следует предусматривать следующие виды hарах legomenа: 

a) слова, однажды встречающиеся в отдельном стихотворении;

б) из hарах legomenа типа а однажды встречающиеся в подгруппе, в 

состав которой входит соответствующее стихотворение;

в) слова, встречающиеся однажды раздельно в каждой подгруппе;

 г) слова, однажды появляющиеся в совокупности, как одном целом, но

которые можем отнести к одной из подгрупп.

 В таблице 7 приведено число отдельных видов hарах 1еgоmеnа с данными в процентном выражении. Они показывают, что процент всех типов hарах  legomenа в переводах ниже, чем в собственных произведениях. Таблица 7

Hарах legomena отдельных типов и их процентная доля в общем числе реализаций слов в соответствующей подгруппе стихотворений Aбая

Тип	Собственные стихотворения	%	Переводы	%
а	1083	54,5	1092	50,5
б	628	31,6	567	26,2
в	585	29,4	486	22,5
г	437	22,0	361	16,7

 

Приведем здесь прогрессию величин, выраженных для х=1, 2, . . . 10, где величины для x = 1 представляют hарах 1еgomena типа в, т. е. число лексических единиц, встречающихся в каждой подгруппе отдельно однажды, дважды и т. д.

 

х	Собственные произведения	Переводы	Знак дифференции
1	585	486	-
2	116	139	+
3	50	68	+
4	28	34	+
5	14	20	+
6	10	10	0
7	13	5	-
8	1	9	+
9	9	5	-
10	6	5	-

 

Рассмотрев дифференцию   можно заметить, что она стремиться к нулю. Следовательно, можно сказать, что между изучаемыми двумя прогрессиями величин не существует значимой разницы.

В результате нашего исследования можно сделать вывод, что в переводах Абая все четыре типа hapax legomena встречаются реже, чем в его собственных произведениях. Тем самым мы уточнили   исследования при помощи характеристики Юла, и показали,  что в языке Абая преобладают  слова, однажды встречающиеся в отдельном стихотворении, что говорит о богатом словарном запасе, и Абай является переводчиком высокого уровня.

Дальнейшее изучение наследия Абая выдвигает задачу углублен­ного специального исследования отдельных сторон его творчества.

 

Форма и рифма в стихах Абая

«Наука только тогда достигает совершенства, когда ей удаётся пользоваться математикой».                                                           К. Маркс.

 

Наибольшие успехи в применении математических методов достигнуты в стиховедении – части поэтики, изучающей принципы организации стиха как формы речи.

Абай выражал свои мысли и эмоции в основном  поэтической форме. Если задаться вопросом  «почему?», то проще и яснее это объяснить математически.

Проза сравнима с нахождением координат на прямой. Мы читаем слово за словом, и они перед нами, как точки на прямой. Смысл текста усваивается «горизонтально» , как и координата у точки на прямой - в одном измерении. А вот поэтический текст  заставляет нас вспоминать конец  или начало предыдущих  строк и сравнивать их, то есть читаем горизонтально и вертикально, а это как система координат на плоскости. А если  поэтический текст «задевает за живое», заставляет думать, то это уже трехмерное пространство.

Поэтому своих произведениях, посвященных искусству слова, песне, Абай утверждает высокое представление о поэзии, высокое понима­ние роли поэта. Придавая большое значение сближению литературы с жизнью, утверждению в ней новых тем, он осуждает развлекатель­ную поэзию, не связанную с насущными проблемами общественной жизни. [2]

О связи математики и поэзии знали ещё в античности. Уже тогда стиховеды  находили простейшие единицы измерения - стопы, затем единицы высшего порядка - стихи, строфы… Они устанавливали  количественные отношения  - долгий слог равен двум кратким.

Изучив учебники по литературе и стихосложению, я выяснила, что стихи имеют меру, как и всё вокруг.

В системах, основанных на оппозиции долготы-краткости гласных, последовательность долгих и коротких слогов сама по себе создавала ритмический образец. Такие повторяющиеся образцы являлись структурными элементами текста и делили его на сегменты:

1. заданная последовательность слогов (обычно от двух до пяти) называлась стопой;
2. заданная последовательность стоп (обычно от четырёх до одиннадцати) называлась стихом;
3. заданная последовательность стихов (обычно от двух до четырёх) называлась строфой. [8]

Стихосложение в его акцентных речевых формах всегда соответствовало трём основным группам или системам стихосложения: силлабической, силлабо-тонической и тонической. Различия в этих группах определяются ритмической основой и соразмерностью, а также повторением ритмических слогов с определённым их расположением внутри строки.

Наше сознание может вести счет длине строк:  или словами, или слогами, или (что уже сложнее) группами слогов – стопами. 
В зависимости от этих мерок мы и различаем системы стихосложения:

Силлабическая система стихосложения (От греч. Syllabe - слог) определяет длину строки по количеству  слогов в строке.  В этом виде стихосложения строки соизмеряются не группами слогов - стопами, а непосредственно слогами.

Тоническая  система (От греч. Tonos - напряжение, ударение.) стихосложения  определяет стих по количеству ударений значащих слов, (в стихе сколько самостоятельных слов – столько и  ударений).

Силлабо-тоническая система стихосложения, в которой ритмичность создается упорядоченностью расположения ударных слогов среди безударных.

В силлабическом стихосложении размер определяется числом слогов;
 в тоническом - числом ударений; 
 в  силлабо-тоническом - метром и числом стоп. [19]

Казахское стихосложение относится к силлабическому.

Понятие «Казахское стихосложение», как категорию теории литературы первым исследовал и обосновал А. Байтурсынов в книге «Әдебиет танытқыш» (1926). Он научно подтвердил теорию казахского стиха, выделяя виды строф, размеры стихотворных строк, стихотворные течения и рифмы, чередование строк. Чтобы отличить ритмику слога от ритмики стиха, он предложил назвать ритмику слога «жорнақ», отмечая, что она создается в зависимости от природы языка тремя путями:

 1) языки, в которых гласные звуки имеют краткость;

2) языки, в которых ударные слоги одинаковые;

3) языки, в которых слоги неодинаковые.

Термины, введенные А. Байтурсыновым в казахское стихосложение:

1) рисунок стиха — «айшық», имеет четыре разновидности;

 2) промежуток между голосовыми волнами, ощущаемый при чтении  

     стиха, — «бунақ»;

3) слог внутри строки — «буын»;

4) граница между голосовыми волнами внутри строки — «кезең»;

 5) порядок стихотворного рисунка — «тармақ» и «шумақ» (строка и

    строфа).

По мнению академика З. Ахметова, в казахских стихах (жыр) издавна чередовались семисложные и восьмисложные строки (4 слога — 3 слога; 3 слога — 2 слога — 3 слога). В народной  поэзии - обычно эпические  дастаны (поэмы) и толгау (размышления) исполнялись в ритме желдирме (речитативное пение), имели семи-восьмисложные строки. При  речитативном  произношении  речевая  интонация  взаимодействует с музыкальной. Напев заметно изменяется, подчиняясь интонационно-синтаксическому построению речи. Произведения в виде больших стихотворных частей назывались «жыр».

Наряду с этим, в народной  поэзии широко использовался одиннадцатисложный стих (4 слога — 3 слога — 4 слога, или 3 слога — 4 слога — 4 слога). Этот размер использовался во время айтысов. [20]

В творчестве Абая выразительные возможности и свойства этого размера проявились с необычайной силой. Одиннадцатисложный стих получает у Абая особую рит­мическую подвижность и гибкость. Это достигалось в значительной мере благодаря тому, что поэт допускал большую свободу во взаимном перемещении в строке первых двух ритмических частей, которые могут со­стоять как из трех слогов, так и из четырех.

При разработке одиннадцатисложного размера Абай уделяет большое внимание сочетанию строк и рифмовке. Особенность формы стиха в одиннадцатисложнике со­ставляет сочетание четырех стихов в строке с объедине­нием одной и той же рифмой первого, второго и четвер­того стихов ааба. Абай с большим мастерством пользуется этой популярной формой одиннадцатисложника. Одно­временно он создает произведения, в которых использует прием монорифмы. Так, в стихотворениях «Қан сонарда бүркітші шығады аңға» («Всадник с беркутом скачет в ранних снегах»), «Қыран бүркіт не алмайды, салса баптап» («Хоть любую добычу беркут берет») и других  поэт использует этот способ, рифмуя стихи далее через строку.

Любопытно при этом отмеченное Е. Исмаиловым яв­ление: в стихотворении «Қан сонарда…» «рифма с окон­чанием «д» и «ға» повторяется все в новых и новых со­четаниях до 50 раз».

Очень  своеобразно применяет Абай прием монорифмы в произведении «Қартайдық, қайғы ойладық, ұйқы сергек» («Вот и старость. Скорб­ны думы, чуток сон»).

 

Строфы	рифма	слоги
Қартайдық, қайғы ойладық, ұйқы сергек, Ашуың - ашыған у, ойың - кермек. Мұңдасарға кісі жоқ сөзді ұғарлық,  Кім көңілді көтеріп, болады ермек?  Жас қартаймақ, жоқ тумақ, туған өлмек, Тағдыр жоқ өткен өмір қайта келмек. Басқан із, көрген қызық артта қалмақ, Бір құдайдан басқаның бәрі өзгермек. Ер ісі - ақылға ермек, бойды жеңбек, Өнерсіздің қылығы өле көрмек. Шыға ойламай, шығандап қылық қылмай,  Еріншек ездігінен көпке көнбек. Жамандар қыла алмай жүр адал еңбек, Ұрлық, қулық қылдым деп қағар көлбек.	а а б а а а в а а а г а а а	3+2+3+2+2=12 3+3+1+2+2=11 4+2+1+2+3=12 1+3+3+3+2=12 1+3+1+2+2+3=12 2+1+2+2+2+2=11 2+1+2+2=2+2=11 1+3+3+2+3=12 1+2+3+2+2+2=12 4+3+2+2=11 2+3+3+2+2=12 3+4+2+2= 11 3+2+2+1+2+2=12 2+2+2+1+2+2=11
Арамдықтан жамандық көрмей қалмас, Мың күн сынбас, бір күні сынар шөлмек.  Адамзат тірілікті дәулет білмек, Ақыл таппақ, мал таппақ, адал жүрмек. Екеуінің бірі жоқ, ауыл кезіп, Не қорлық құр қылжаңмен күн өткізбек?  Наданға арам - ақылды құлаққа ілмек, Бұл сөзден ертегіні тез үйренбек. Рас сөздің кім білер қасиетін, Ақылсыз шынға сенбей, жоққа сенбек.  Қызыл арай, ақ күміс, алтын бергек Қызықты ертегіге көтерілмек. Ақсақалдың, әкенің, білімдінің, Сөзінен сырдаң тартып, тез жиренбек. Ақылды қара қылды қырыққа бөлмек, Әр нәрсеге өзіндей баға бермек.	д а а а е а а а ж а а а ж а а а	4+3+2+2=11 1+1+2+1+2+2+2=11 3+4+3+2=12 2+2+1+2+2+2=11 4+2+1+3+2=12 1+2+1+3+1+3=11 3+2+3+3+2=13 1+2+4+1+3=11 1+2+1+2+4=10 3+2+2+2+2=11 2+2+1+2+2+2=11 3+4+4=11 4+3+4=11 3+2+2+1+3=11 3+2+2+3+2=12 1+3+3+2+2=11
Таразы да, қазы да өз бойында, Наданның сүйенгені - көппен дүрмек.  Алашқа іші жау боп, сырты күлмек, Жақынын тіріде аңдып, өлсе өкірмек. Бір-екі жолы болған кісі көрсе, Құдай сүйіп жаратқан осы демек. Ел бұзылса, құрады шайтан өрмек, Періште төменшіктеп, қайғы жемек. Өзімнің иттігімнен болды демей, Жеңді ғой деп шайтанға болар көмек. Сырттансынбақ, қусынбақ, өршілденбек, Сыбырменен топ жасап бөлек-бөлек. Арамдықпен бар ма екен жаннан аспақ,  Өзімен өзі бір күн болмай ма әлек? Қолдан келе бере ме жұрт меңгермек,  Адалдық, арамдықты кім теңгермек? Мақтан үшін қайратсыз болыс болмақ, Иттей қор боп, өзіне сөз келтірмек.	з а а а и а а а к а а а л а а а л  а	3+1+2+1+1+3=11 3+4+2+2=11 3+2+2+1+2+2=12 3+3+2+2+3=13 1+2+2+2+2+2=11 2+2+3+2+3=12 1+3+3+2+2=11 3+4+2+2=11 3+4+2+2=11 2+1+1+3+2+2=11 4+3+4=11 4+1+2+2+2=11 4+1+1+2+2+2=12 3+2+1+1+2+1+2=12 2+2+2+1+1+3=11 3+4+1+3=11 2+2+3+2+2=11 2+1+1+3+1+3=11
n=48 – генеральная совокупность строф мода= 11 размах= 3 медиана= 11	n=48 а-36	К-во слогов К-во строф 11 30 12 15 13 2 10 1

Здесь все произведение целиком строится на од­ной рифме, притом рифма в каждом четверостишии пов­торяется троекратно. Монорифма  используется им в необычайно сконцентрированном виде. В стихотворении «Қартайдық, қайғы ойладық, ұйқы сергек»  на 48 стихов приходится 36 одинаковых рифм! К тому же, как заметил еще Б. Кенжебаев, ни одно слово в этом стихотворении не повторяется в рифме дважды, в рифму ставятся все но­вые и новые слова. [21]

Абай обнаруживает совершенное владение размером (жыр’а) стиха  и в стихотворении «Келдік талай жерге енді».

 

			Рифма	Строфы
Келдік талай жерге енді,	а	2+2+2+2=8
Кіруге-ақ қалдық көрге енді.	а	3+1+2+2+2=10
Қызыл тілім буынсыз,	б	2+2+3=7
Сөзімде жаз бар шыбынсыз,	б	3+1+1+3=8
Тыңдаушымды ұғымсыз	б	5+3=8
Қылып тәңірім берген-ді.	а	2+3+2+1=8
Осы жасқа келгенше,	в	2+2+3=7
Өршеленіп өлгенше,	в	4+3=7
Таба алмадық бір адам	г	2+3+1+2=8
Біздің сөзге ергенді.	а	2+2+3=7
Өмірдің өрін тауысып,	д	3+2+4=9
Білімсізбен алысып,	д	4+3=7
Шықтық міне белге енді.	а	2+2+2+2=8
Енді аяңда, жығылма,	ж	2+3+3=8
Сыймас жерге тығылма,	ж	2+2+3=7
Қой бұрынғы желгенді!	а	1+3+3=7
Қайғы шығып иыққа,	з	2+2+3=7
Қамалтпасын тұйыққа,	з	4+3=7
Сергі, көңілім, сергі енді!	а	2+3+2+2=9
Балапан құстай оңдалып,	д	3+2+3=8
Қанатыңды қомданып,	д	4+3=7
Жатпа ұяда қорғанып,	д	2+3+3=8
Ұш, көңілім, көкке, кергі енді!	а	1+3+2+2+2=10
Көңілде қайғы, қалың зар,	к	3+3+3+1=10
Айтатұғын сөзім бар,	к	4+2+1=7
Салсын құлақ ұққандар,	к	2+2+3=7
Өрбі, сөзім, өрбі енді!	а	2+2+2+2=8
Іште қайғы дерт пысып,	д	2+2+1+2=7
Көкіректі өрт қысып,	д	4+1+2=7
Айтуға көңілім тербенді.	а	3+3+3=9
Өзің жалғыз, надан көп,	л	2+2+2+1=7
Ұқтырасың сен не деп,	л	4+1+1+1=7
Әулекі, арсыз елге енді?	а	4+2+2+2=10
Тыныштық сүймей қышынып,	д	3+2+3=8
Өтірікке тұшынып,	д	4+3=7
Пәледен тұрмас шошынып,	д	3+2+3=8
Тұл бойын желік жеңген-ді.	а	1+2+2+2+1=8
Туған жерді қия алмай,	м	2+2+2+2=8
Тентекті жеңіп, тыя алмай,	м	3+2+2+2=9
Әлі отырмыз ұялмай,	м	2+3+3=8
Таба алмадық өңге елді.	а	2+3+2+2=9
Әзелде тәңірім сорлы етті	н	3+3+2+2=10
Арсыз елмен әуре етті,	н	2+2+3+2=9
Жалғыз үйде күңірентті,	н	2+2+4=8
Тағдырға білдік көнгенді.	а	3+2+3=8
Адам деген даңқым бар,	к	2+2+2+1=7
Адам қылмас халқым бар,	к	2+2+2+1=7
Өтірік пен өсекке	е	3+1+3=7
Бәйге атындай аңқылдар —	к	2+3+3=8
Тұла бойым шіміренді.	а	2+2+4=8
Барма топқа шақырмай,	м	2+2+3=7
Жат үйіңде шатылмай,	м	1+3+3=7
Шыдармын ба, япырмай,	м	3+1+3=7
Жатуға шықпай үйде енді?	а	3+2+2+2=9
Қатыныңның ойнасын	т	4+3=7
Көрсең, білсең қоймасын,	т	2+2+3=7
Не ойлар едің өз басың,	т	1+2+2+1+2=8
Сонымен тең біз де енді.	а	3+1+1+1+2=8
АБАЙ ҚҰНАНБАЙҰЛЫӨЛЕҢДЕРҚАЗАҚША ӨЛЕҢАБАЙ ӨЛЕҢДЕРІАБАЙЖЕРКЕЛДІК ТАЛАЙ ЖЕРГЕ ЕНДІАБАЙ ҚҰНАНБАЙҰЛЫ ӨЛЕҢДЕРІ

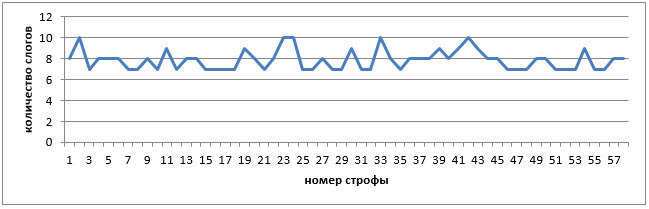
Группировка стихов и последовательность рифм осуще­ствлены в этом произведении более строго, чем это быва­ет обычно в стихе. Основная рифма возвращается в большинстве случаев через три, несколько реже – через два стиха. Эти три или два стиха связываются каждый раз одной новой рифмой. И что очень характерно, в риф­ме участвуют все 58 строк стихотворения за исключением всего лишь двух стихов. Между тем в жыр’е(форме)  стихи, оста­ющиеся вне рифмы обычно встречаются более часто. Причем сквозная рифма(енді)  повторяется в стихотворении Абая 17 раз!

В поисках новой выразительности стихотворной речи, в формах семисложного и семи-восьмисложного стиха поэт своеобразно применяет наряду с традиционной в казахской народной поэзии рифмой через строку абаб – «Кешегі Оспан ағасы» («Труд чужой Оспан ценил»),

				К-во слогов
Кешегі Оспан ағасы	б	3+2+3=8
Кісінің малын жемепті.	а	3+2+3=8			16
Мал сұраған кісіге	б	1+3+3=7
Жоқ, қайтемін демепті.	а	1+3+3=7		30	14
Қуаты артық, ойы кең,	б	3+2+2+1=8
Жұрттың бәрін шенепті.	а	2+2+3=7			15
Досына дәл жаз, жауға аяз,	б	3+1+1+3+2=9
Алысқанды денепті.	а	4+3=7		31	16
Адалдық үшін алысып,	б	3+2+3=8
Жегішке ақы төлетті	а	3+2+3=8			16
Бас шайқаймын дегеннің.	б	1+3+3=7
Басына салды әлекті.	а	3+2+3=7		30	14
Қадірі қалың, малы көп,	б	3+2+2+1=8
Қылмаған кімге себепті?	а	3+2+3=8			16
Алақолсыз мырза еді,	б	4+2+2=8
Кем-кетікті елепті.	а	1+3+3=7		31	15
Оны да алды бұл өлім,	б	2+1+2+1+2=8
Сабырлық қылсақ керек-ті.	а	3+2+2+1=8			16
	14                     14           15                15           16 16 16 16 16  N=9              мода =16 размах =2 медиана =16		30 31 30 31 N=4 Мода =30 и 31 Медиана =30,5 Размах=1

 

Заман ақыр жастары,		а	2+2+3=7
Қосылмас ешбір бастары.		а	3+2+3=8
Біріне бірі қастыққа		б	3+2+3=8
Қойнына тыққан тастары.		а	3+2+3=8	31
Саудасы – ар мен иманы,		а	4+1+1+3=8
Қайрат жоқ бойын тыйғалы.		а	2+1+2+3=8
Еңбекпен етті ауыртпай,		б	3+2+4=9
Құр тілменен жиғаны.		а	1+3+3=7	32
Өнімсіз іске шеп-шебер,		а	3+2+1+2=8
Майданға түспей несі өнер?		а	3+2+2+2=9
Сиырша тойса мас болып,		б	3+2+1+2=8
Өреге келіп сүйкенер.		а	3+2+3=8	33
Күлмеңдеп келер көздері,		а	3+2+3=8
Қалжыңбас келер өздері.		а	3+2+3=8
Кекектеп секек етем деп,		б	3+2+2+1=8
Шошқа туар сөздері.		а	2+2+3=7	31
	31 32 33 31                 N =4 Мода = 31 Медиана =31,5 Размах =2   Асимметрия

 

 «Бермеген құлға қайтесің» («Не так силен человек»), «Жылағанды тоқтатып» («Магиш, родная не плачь») и дру­гие – не менее характерную для казахского поэтическо­го творчества строфу – четверостишие с рифмой ааба – «Заман ақыр жастары» («Погляди на молодежь»), «Айттым сәлем, қалам қас» («Шлю, тонкобровая, привет»).

Кроме того, во многих произведениях, в которых ис­пользована форма четверостишной строфы, он вводит перекрестную рифму абаб. Например, в стихах «Менсінбеуші ем наданды» («Я гордо презирал невежество и тьму»), «Әсемпаз болма әрнеге» («Будь разборчив в пу­ти своем»), «Не іздейсің, көңілім, не іздейсің?» («Что ты ищешь, моя душа?»).

Эти способы рифмовки он внед­ряет также и в шестисложный стих.

Заслуга Абая, впервые применившего в коротких сти­хах перекрестную рифму, была специально отмечена И. Джансугуровым в особой статье о художественном мастерстве поэта. Представляет интерес также приме­нение Абаем междустрофной рифмы, которая связывает не одну, а целый ряд строф. Еще в произведении «Иузи – рәушан, көзі – гәуһәр» («Как яхонт, взором ты мила»), относящемся к числу первых стихотворных опы­тов юношеского периода, в которых молодой поэт вос­создает поэтическую манеру классиков восточной поэ­зии, находим рифму аааб. Здесь использована рифма четверостишной формы с одинаковой концовкой в первых трех стихах и единой общей рифмой для последней строки всех строф.

Междустрофную рифму этого типа Абай употребля­ет позже в стихотворении, написанном семисложным стихом, – «Білімдіден шыққан сөз» («Да будет слово мудреца»). Первая строфа имеет рифму ааба, обычную для казахской поэзии. Все другие семь строф стихотво­рения рифмуют так, что в конечном стихе каждой строфы дают возвращение рифмы первой строфы. А другие три стиха в них объединяются каждый раз одной особенной рифмой.

Білімдіден шыққан сөз Талаптыға болсын кез. Нұрын, сырын көруге, Көкірегінде болсын көз. Жүрегі - айна, көңілі - ояу, Сөз тыңдамас ол баяу. Өз өнері тұр таяу, Ұқпасын ба сөзді тез? Әбілет басқан елерме, Сөзге жуық келер ме? Түзу сөзге сенер ме, Түзелмесін білген ез? «Айтшы айтшылап» жалынар, Ұққыш жансып шабынар. Ұқпай жатып жалығар, Ұйқылы-ояу бойкүйез. Жас баладай жеңісқой, Байлаулы емес ақыл, ой. Ойлағаны - айт пен той, Ыржың-қылжаң ит мінез. Сұлу қыз бен я батыр Болмаған соң , тәңірі алғыр, Шығып кетер, я қалғыр, Оған ақыл - арам без. Жақсыға айтсаң, жаны еріп, Ұғар көңіл шын беріп, Дертті ішіне ем көріп, Неге алтынды десін жез. «Ой, тәңір айшыл» кер есек, Қулық, сұмдық не өсек Болмаған соң, бір есеп - Мейлі қамқа, мейлі бөз.	а а б а   в в в а   в в в а   в в в а   в в в а   в в в а   в в в а   в в в а	4+2+1=7 4+2+1=7 2+2+3=7 5+2+1=8   3+2+3+3=11 1+3+1+3=8 1+3+1+3=8 3+1+2+1=7   3+2+3=8 2+2+2+1=7 2+2+2=1=7 4+2+1=7   2+3+3=8 2+2+3=7 2+2+3=7 3+3+3=9   1+3+3=7 4+2+2+1=9 4+1+1+1=7 2+2+1+2=7   2+1+1+1+2=7 3+1+3+2=9 2+2+1+2=7 2+2+2+1=7   3+2+2+2=9 2+2+1+2=7 2+3+1+2=8 2+3+2+1=8   1+2+2+1+2=8 2+2+1+2=7 3+1+1+2=7 2+2+2+1=7	29         34         29         31         30         30         32         29
			29      n=8 29    мода=29 29      30 30 31 32 34 Размах= 5 медиана=30

 

Таким образом, новаторство Абая в работе над сти­хом в большой мере проявилась в разнообразном приме­нении стихотворных размеров и форм казахской поэзии, многие из которых он подверг в той или иной степени творческой обработке, обогатив при этом способы и при­емы их употребления.

Большинство из них, несмотря на то, что они имеют ритмическую форму с более сложным по характеру со­четанием стихов и слоговыми соотношениями, обладает предельной простотой, ясностью и легкостью структуры. Вместе с тем в отдельных случаях поэт создает услож­ненные стихотворные формы с применением трудного строфического рисунка, которые требуют для своего употребления исключительного поэтического, в частно­сти технического мастерства.

С точки зрения образования новой формы небезынтересен размер стихотворения «Бай сейілді» («Звереет бай»).

  

		Рифма	Количество слогов		Количество слогов		Рифма
Бай сейілді,		а	1+3=4	Звереет бай,	3+1=4		а
Бір бейілді,		а	1+3=4	Скудеет край	3+1=4		а
Елде жақсы қалмады,		б	4 + 3= =2+2+3=7	Людьми с хорошею душой .	2+3+2=7		б
Елдег (і) еркек		в	2+2=4	Правитель тут –	3+1=4		в
Босқа селтек		в	2+2=4	Презренный плут,	3+1=4		в
Қағып, елін қармады.		б	4 + 3 = =2+2+3=7	Народ обирает свой.	2+4+1=7		б

                                                    

Особенностью этой стихотворной формы является сочетание в ней коротких строк с длинными. Кроме того, ритмическая обособленность ко­ротких стихов подчеркивается также рифмой.

В целом ритм стиха получает большую подвижность, легкость. Графически  это похоже на синусоиду, что подтверждает гармонию звука.

В произведении «Ем таба алмай» («Не продохнуть»), в котором ритм в общем строится на тех же основах.

		Слоги
Ем таба алмай, От жалындай Толы қайғы кеудеге Сырлас(а)алмай                         Сөз аш (а) алмай Бендеге.	а а б а а б	4 4 4 + 3 =7 4 4  3	Симметрия до 5 строфы

 

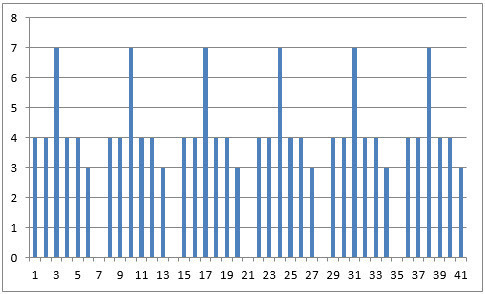
Это – шестистрочная строфа, в которой третий стих семисложный, шестой стих – трехсложный, а все ос­тальные – четырехсложные.

Рифма  аабввб в этом стихе снимает излишнюю симметрию структуры строфы, а четырехслож­ные стихи, параллельны по ритму.

Приемы стихосложения, которые Абай творчески при­менял в рассмотренных выше размерах, нашли новое блестящее воплощение в его произведении «Сегіз аяқ» («Восьмистишия»).

Название размера, равно как и самого произведения, установилось по числу стихов в строфе. Это, очевидно, объясняется тем, что форма восьмистишной строфы вос­принималась как новая, несколько необычная.

Стихотворение состоит из 25 строф-восьмистиший.

И в целом стихотвор­ная форма «Восьмистиший» как со стороны строфиче­ской композиции стиха, так и ритмического его построе­ния, является едва ли не самым замечательным откры­тием Абая в области стихосложения.

И самое замечательное в том, что Новая ритмическая форма вырастает у Абая из соединения в поэтических строках широко употребительных в казахской поэзии двух-, трех-, четырехслоговых частей. Сочетание таких ритмических частей предстает в «Восьмистишиях» в не­повторимо новом, своеобразном претворении. Стихотвор­ные строки включают в себя разное

число ритмических частей: восьмисложные – три, а семисложные и пяти­сложные – две. Чередование их создает в процессе дви­жения стиха непрерывную смену ритма, придает стиху необычайную гибкость и виртуозность. В первых трех строках имеет место ритмический переход от пятислож­ных строк к семи- или восьмисложной. Сначала следу­ют две короткие пятисложные строки, одинаковые по структуре. Затем идет более длинная семи- или же вось­мисложная строка.

Эта структура повторяется и в последующих трех сти­хах, чем значительно усиливается наметившаяся в пер­вой части инерция ритма. Таким образом, в этих шести строках стиха переход от коротких строк к более длин­ным обозначен четко, однако, общая тональность ритми­ки определяется прежде всего пятисложными строками, которые решительно преобладают… И лишь двухкратное повторение длинных – семи- и восьмисложных – строк в концовке, резко усиливающее ритм длинных строк, придает законченный характер перемене в движении ритма. Как видим, конец строфы дает новую смену рит­ма. Однако возникновение ее глубоко закономерно. Строки из семи или же восьми слогов дважды встреча­лись в строфе еще до этого в конце ее трехстишных ча­стей, чем оправдано появление таких же строк в замы­кающем строфу двустишии.

Тонкая разработанность стихотворной формы «Вось­мистиший» предстанет перед нами полнее, если ближе присмотреться к ее строфическому оформлению.

Он применяет весьма сложную   систему   рифмовки: аа б вв б гг.

Показательно уже то, что в стихе на восемь строк приходится четыре различных рифмы. Причем охватыва­ются рифмой все строки строфы без исключения. И дело не только в том, что четырехрифменная строфа была новостью в казахской поэзии, очень интересен самый ход рифм.

В трехстишиях короткие строки рифмуются попарно. Этим как бы отмечается параллельность ритмических рядов, в то же время рифма указывает на тесное объеди­нение смежных коротких строк в ритмико-интонационном отношении. Несомненно, что в этих стихах парная рифма более всего уместна. Она ритмически сближает короткие стихи, ярко оттеняет их одинаковую ритмиче­скую структуру, усиливает их звучность. Кроме того, в трехстишии две короткие строки связаны парной риф­мой, а третья – длинная строка, не созвучна с ними, что вносит известное ритмическое равновесие и стройность в структуру строфы. Это полностью отвечает тому, что в ритмическом отношении два коротких стиха противостоят одному длинному.

Однако два соседних коротких стиха в каждом из трехстиший имеют свою парную рифму: первая и вторая строки связаны одной парной рифмой, а четвертая и пя­тая – другой. Очевидно, что это продиктовано желани­ем достигнуть разнообразия и богатства звуковой гармо­нии. Сходство в созвучии ритмических рядов соблюдает­ся лишь в той мере, в какой это необходимо, чтобы до­биться отчетливости общего ритмического движения стиха.[ 2]

 ЗАКЛЮЧЕНИЕ

Подведём итог нашему исследованию:

Математика и поэзия не так далеки как кажется на первый взгляд. И обе как одно целое помогают друг другу создавать гармонию в окружающем мире.

Каждый язык имеет свою частотность применения букв и слов, что позволяет определить характерные особенности этого языка.

Предполагается что стихи это песни, но без музыки. Почему же некоторые стихи приятны слуху, а некоторые нет. Это зависит от рифмы.

Применив математические методы к исследованию творчества великого казахского поэта Абая (Ибрагима) Кунанбаева можно  определить принадлежность вновь найденных произведений к перу поэта и просветителя.

Язык Абая отличается богатством стилистических оттенков, большим разнообразием интонационно-синтак­сической структуры речи, простотой, легкостью и гибко­стью синтаксических конструкций.

Абай не просто обогатил казахский поэтический язык, но и показал способы и приемы творческого использова­ния богатств народного языка в поэзии.

Это исследование обогатило моё представление о литературе и особенно казахской. Я узнала много нового и интересного о применении математических методов. Думаю продолжать свои исследования в направлении применения математики.

ЛИТЕРАТУРА

1. Абай.  Стихи.  Алматы:  Жарын,  1994.  —  320  с. 
2. Ахметов З. РОЛЬ АБАЯ В РАЗВИТИИ КАЗАХСКОГО СТИХОСЛОЖЕНИЯ.   https://www.kazportal.kz/
3. Бертельс Е.Э.Суфизм и суфийская литература. М.,1965 
4. В. М. Жирмунский «Введение в метрику» Изд. "Academia". Л., 1925, стр. 85 — 86.)
5. Белгер Герольд .Гармония духа. - М.: Русская книга, 2003. -288 с.
6. Вейль Г. О философии математики. - М.: ГИТТЛ, 1934. - 128 с.
7. Л.Гржебич  «О некоторых количественных свойствах лексики Абая» Международный клуб Абая 2004г с 29-30
8. Материал из Википедии — свободной энциклопедии
9. Назарбаев Н.А. "Третья модернизация Казахстана: глобальная конкурентоспособность"послание от  31.01 2017г
10. Нүрсүлганов. Ф Бүоіанова. Шәкәрімнід абая и логико - философских мүрасы сегодня в школе. вестник (Вестник КазГУ - N2 (5), 2000 г.... С 19 по 25 страницы.
11. СТИХОСЛОЖЕНИЯ http://abai-inst.kz
12. Сухотин А.К. « Ритмы и алгоритмы» М 1985 г
13. Фасмер, ИОРЯС 12, 2, 279; Гр.-сл. эт. 192; Мi. ЕW 323.
14. Энциклопедия. – Алматы: «Қазақ энциклопедиясының» Бас редакциясы, «Атамұра» баспасы, ISBN 5-7667-2949-9
15. Энцикопедия http://knowledge.su
16. http://www.heritagenet.unesco.kz/kz/content/history/portret/abay.htm
17. /xreferat.com/31/1403-1-vzaimodeiystvie-matematiki-i-yazykoznaniya.html
18. https://www.nur.kz  Сколько слов в казахском языке?
19. © Copyright: Творческая Мастерская Алкоры, 2012
20. https://e-history.kz/ru/contents/view/3549
21. http://abai-inst.kz