Павлова Екатерина Вячеславовна, 4 «Б» класс, МАОУ Гимназия № 13, г. Екатеринбург, Свердловская область, Россия
Научный руководитель: Дорожкина Вероника Петровна, учитель математики, МАОУ Гимназия № 13, г. Екатеринбург, Свердловская область, Россия
Исследовательская работа "Математика и музыка"
Введение
Актуальность темы.
Есть ли что-то общее между математикой и музыкой? Присутствует ли математика в музыке? Изучались ли звуки с математической точки зрения? Данные вопросы возникли давно. Исследованию музыки посвящали свои работы многие великие математики. Так как я учусь в музыкальной школе, мне тоже стало интересно рассмотреть эту связь, найти общее между математикой и музыкой, изучить музыку с точки зрения математики. Поэтому я выбрала эту тему для моего исследования и решила заняться им углубленно.
Цель работы: Выявление общих черт между математикой и музыкой, подтверждение присутствия математики в музыке.
Задачи работы:
- изучить литературу по теме исследования;
- узнать, были ли в истории попытки связать математику и музыку;
- выявить общие свойства между математикой и музыкой;
- сделать выводы.
Методы:
- сбор информации;
- изучение литературы;
- подбор фактов и примеров, подтверждающих связь между математикой и музыкой;
- сравнительный анализ;
- собственный опыт в музыкальной школе.
Карл Гаусс утверждал, что «математика – царица всех наук». Математика является базой для всех остальных областей. В древности ученые рассматривали математику как составную часть философии, которая служила средством познания и объяснения окружающего мира. В настоящее время такой позиции придерживается автор учебников по алгебре, Александр Георгиевич Мордкович, который относит математику к гуманитарным предметам, с помощью которых происходит познание окружающего мира.
Математика изучает количественные закономерности, присущие всем предметам и явлениям действительности. Математика предлагает четкие и логические модели для изучения окружающей действительности, для описания явлений в природе, технике, обществе. При исследовании, математическая модель изучаемого объекта может дать новую информацию и позволяет найти закономерности.
Проникновение математики и ее методов в другие области науки и искусства является формой их взаимодействия. Оно способствует сближению различных отраслей знаний, процессу их математизации. Одной из особенностей данного процесса является ее универсальность, проявляющаяся в проникновении математических методов во все сферы жизни людей, начиная от решения бытовых задач и до технического прогресса. Многие области науки (физика, химия, медицина, электроника, строительство, космонавтика) не могут обойтись без математического аппарата, без использования специальных математических терминов.
Математика всегда была неотъемлемой частью человеческой культуры, средством познания всего окружающего мира. Искусство также может иметь свою теорию, которую можно выразить в терминах математики. Попытки найти математические закономерности и использовать математику в искусстве и культуре были с древних времен (в скульптуре: система пропорций человеческого тела; в архитектуре: симметрия зданий, математические расчеты в конструкциях, построениях, пирамиды, геометрические фигуры, как модель для архитектурных форм; в живописи: теория перспективы, геометрические законы построения; в музыке: учение Пифагора о звуках)
Попытки найти математику в других областях были совершены и описаны раньше. Целью моей работы будет являться поиск и выявление общих свойств и связей между музыкой и математикой.
Слово «математика» – древнегреческого происхождения, означает изучение, знание, наука. В словаре В.И.Даля, под математикой понимается все, что можно выразить цифрою, принадлежит математике.
По мнению Декарта к области математики относят те науки, в которых рассматривается либо порядок, либо мера, и совершенно не существенно, будут ли это числа, фигуры, звезды, звуки или что-нибудь другое, в чем отыскивается эта мера.
Математика – это наука о числах, величинах, их свойствах, законах их соединения, количественных отношениях и пространственных формах. Основу математики составляют величины, количественные отношения, формулы, которые в свою очередь состоят из чисел.
Исторически математика появилась под воздействием необходимости: вести расчёты при измерении земель, скота, для решения задач в бытовой жизни, в торговле, в астрономии, в мореплавании, для строительства и для решения многих других задач. Для решения поставленных задач люди начали широко пользоваться математикой. Ведь всюду, где надо что-то считать, измерять, сравнивать, без математики не обойтись. Она нужна и важна всем. Ведь все, что можно измерить, выразить числом, становится материалом для применения математики. Математика – фундаментальная наука, предоставляющая общие языковые средства другим наукам.
Слово «музыка» (с греч. «муза» ) – обозначает «искусство муз». В греческой мифологии музы – это покровительницы областей культуры. Считается, что именно в Древней Греции музыка достигла наивысшего расцвета в культуре Древнего мира. Музыка как предмет образования и воспитания имела огромное значение для греков и в целом для всей цивилизации.
Музыка – это вид искусства, художественным материалом которого является звук; это искусство организации звуков. Звуки – это необыкновенный, невидимый материал, из которого создается музыка.
В мире существует много видов искусств: живопись, музыка, архитектура, скульптура и многие другие. По моему мнению, музыка занимает основную позицию в этом ряду. Музыка – одно из главных проявлений культуры, охватывающее все страны и все эпохи. Она вызывает различные эмоции и образы у человека, она волнует и дарит наслаждение, вызывает душевную радость или грусть, поднимает боевой дух, бодрит или успокаивает. Она входит в жизнь человека и интересна многим. Музыка – искусство очень древнее, без нее не мог жить ни один народ на земле. Она звучит с давних времен. Музыкальные инструменты существовали еще в доисторические времена. Например, уже тогда были изобретены разнообразные ударные инструменты, бубны, трубы, флейты. Это доказывает, что первые мелодии были придуманы еще в древности.
В музыке используются такие понятия, как ритм, лад, мелодия, регистр, гармония, тембр. Эти элементы присущи всем музыкальным произведениям: и простым, и самым сложным. Из этого складывается язык музыки.
Люди уже давно задумывались о связи между музыкой и математикой. Исследованию музыки посвящали свои работы многие великие математики:
- Рене Декарт («Трактат о музыке»),
- Леонард Эйлер («Диссертация о звуке»);
- Готфрид Лейбниц,
- Христиан Гольдбах,
- Жан Д'Аламбер,
- Даниил Бернулли и другие.
Первым ученым-математиком, отличившимся в музыкальной сфере, был Пифагор. Он жил в 6 веке до нашей эры в Греции. Музыка для Пифагора стала не только средством вдохновения (страсть к музыке он сохранил всю жизнь), а предметом научных изысканий. Великий древнегреческий ученый был не только математиком, философом, но и творцом акустики и основоположником теории музыки. Он был первым, кто изучил, нашел и установил связь между музыкой и математикой. Пифагор создал учение о звуке, математически установил музыкальные гармонии созвучий.
Однажды, проходя мимо кузнецы, Пифагор случайно услышал, как удары молота создают определенные созвучия. После этого он занялся экспериментами, пытаясь найти соотношения между высотой звука и числами. Он открыл числовые соотношения между отдельными звуками и занялся поисками гармонических интервалов.
Первым музыкальным инструментом Пифагора был однострунный монохорд, который явился предком фортепиано. Пифагор отметил определенное соответствие высоты звука и длины струны. При изменении длины струны изменялась звучащая нота: чем короче струна, тем выше нота, т.е. короткая струна издает высокий звук. И наоборот: чем длиннее натянутая струна, тем ниже звук.
При одновременном звучании нескольких нот (звуков с различной высотой) получаются созвучия: интервалы, аккорды. Если таких звуков 2, то созвучие называется интервалом. Т.е. интервал - это расстояние, разность между двумя соседними звуками. Одновременное сочетание 3-х и более звуков образует аккорд. В музыке созвучия делятся на: консонансные (приятные на слух, гармоничные) и диссонансные (неприятные, резкие).
На примере струнного музыкального инструмента Пифагор выявил: для того, чтобы струны при игре звучали «согласно», гармонично и приятно для уха, длины звучащих частей струн должны быть в определенном отношении. Пифагор установил и математически доказал эти соотношения. Он первым обнаружил приятные на слух созвучия – консонансы, которые получаются лишь в том случае, когда длины струн относятся друг к другу как определенные целые числа, т.е. находятся в правильном численном отношении друг ко другу. Например, эти соотношения: 1:2, 2:3, 3:4, которые относятся к таким благозвучным интервалам, как октава, квинта, кварта. Это явилось доказательством существования числовых закономерностей в природе. Пифагор первым пытался выразить красоту музыки с помощью чисел.
Он также пытался связать музыку с астрономией, развил учение о врачевании болезней при помощи музыки.
Затем последователи Пифагора (пифагорейцы) и другие математики проявляли интерес к музыке. На протяжении столетий в развитии европейской культуры музыкальное образование было востребовано. Музыку изучали наряду с другими науками. Еще не была сформирована математическая наука, но в музыкальном ритме человеку открылись сущность пропорций и симметрии. Еще не было науки геометрии, но в мелодиях, которые пел человек, уже было представление о существовании «верха» и «низа», о разных точках пространства, которые обозначали разные по высоте звуки. Со временем обнаружили и другие элементы математики, которые присутствуют в музыке.
Рассмотрим теперь конкретно, что есть общего у математики и у музыки, общие элементы и свойства.
Использование символов для записи.
В музыке нотная запись читается слева направо, подобно тому, как читаются тексты, написанные на западных языках. На письме, чтобы записать слова, мы используем буквы. В математике, чтобы записать числа, мы используем цифры. А в музыке для записи звуков и мелодий используют такие символы, как ноты. Любую музыку можно записать с помощью 7 нот, расставляя около них музыкальные знаки. Аналогично и в математике: 10 цифр позволяют записать любые числа, и используются свои знаки.
Сходство между математикой и музыкой проявляется в использовании общих символов, знаков и цифр. Некоторые математические символы и знаки используются и в музыкальной записи. Например:
- стрелочки «вверх» ( ↑ ) или «вниз» ( ↓ ) используются для обозначения повышения или понижения музыкальной ступени лада, движения мелодии вверх или вниз, восходящих или нисходящих интервалов;
- знаки неравенства «больше» ( > ) или «меньше» ( < ) используются для обозначения уменьшения (диминуэндо) или усиления (крещендо) громкости звука;
- стрелочки «вправо-влево» ( ↔ ) используются для обозначения операции обращения одних музыкальных интервалов в другие;
- латинские буквы (А,В,С,D,E,F,G,H) используются для обозначения нот, аккордов, тональностей;
- цифры используются для многих обозначений.
Использование цифр для записи.
Цифры, которые используют в математике, как арабские, так и римские, встречаются и в музыке. Например, цифрами в музыке обозначают:
- музыкальный размер произведения, выраженный дробью (2̸4, 3 ̸4, 1̸2, 6̸ 8…),
- номера ступеней лада (I, II, III, IV, V, VI, VII),
- аппликатуру у нот, т.е. позицию (номер) пальцев рук на разных струнах или клавишах (1–большой палец, 2–указательный, 3–средний, 4–безымянный, 5–мизинец),
- номера октав, расположенных в порядке возрастания по высоте звука (1-ая октава, 2-ая октава, 3-я октава и т.д. Причем, например, 5-ая октава звучит выше, чем предыдущие 1-ая, 2-ая, 3-я, 4-ая октавы),
- интервалы и аккорды (ч.1, м.2, б.2, м.3,б.3,ч.4…, Т6 4, S3 5, D3 4 …),
- количество тонов и полутонов в интервалах (ч.1- 0 тонов, м.2 - 1̸2 тона, б.2 – 1 тон, м.3 - 1 1̸2 тона, б.3 - 2 тона, ч.5 – 4 1̸2 тона, м.7 - 5 тонов, ч.8 - 6 тонов…).
Цифры, встречающиеся в названии музыкальных интервалов и аккордов, показывают, сколько ступеней содержит данный интервал или аккорд. Например, интервал ч.4 (чистая кварта) содержит в себе 4 тона или 8 полутонов. Причем, в названиях интервалов и аккордов в музыке используют термины из математики.
Примеры названия интервалов: 1-прима, 2-секунда, 3-терция, 4-кварта, 5-квинта, 6-секста, 7-септима, 8-октава. Среди интервалов различают: большие и малые, увеличенные и уменьшенные интервалы.
Примеры названия аккордов: трезвучие (Т3 5, S3 5, D3 5 …), секстаккорд (Б6, М6), квартсекстаккорд (Б4 6 , М4 6…), секундаккорд (D2 …), септаккорд (D7 …), квинтсекстаккорд (D5 6 …), терцквартаккорд ( D3 4 …) и др.
Для наглядности, как и в математике, данные сводятся в таблицы.
Например, таблица интервалов.
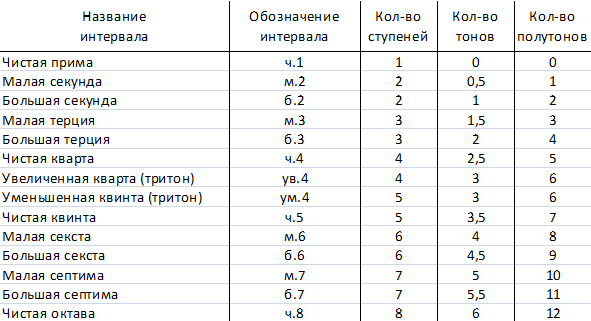
Использование формул.
В музыке так же, как и в математике, используются формулы и определенные зависимости. Например, существуют: формулы строения мажорной и минорной гаммы, формулы длительностей нот, формулы аккордов, формулы септаккордов и др.
Примеры формул аккордов:
Б3 5 = б.3+м.3 Б6 = м.3+ч.4
М3 5 = м.3+б.3 М6 = б.3+ч.4
Ув.3 5 = б.3+б.3 Б4 6 = ч.4+б.3
Ум.3 5 = м.3+м.3 М4 6 = ч.4+м.3
К примеру, формула Б3 5 = б.3+м.3 означает строение мажорного трезвучия, которое состоит из двух интервалов: большой терции и малой терции.
Примеры формул септаккордов:
D7= Б3 5+м.3= б.3+м.3+м.3
D6 5 = Ум.3 5+б.2 = м.3+м.3+б.2
D4 3= м.3+б.2+б.3
D2= б.2 + Б.3 5 = б.2+б.3+м.3
К примеру, формула D7 = Б3 5+м.3 = б.3+м.3+м.3 обозначает строение септаккорда, который состоит из мажорного трезвучия и интервала малой терции, или это можно представить в виде суммы трех интервалов: большой терции, малой терции и малой терции.
Физика звука.
Музыка – это набор звуков. Звуки имеют различные параметры. Если рассмотреть звук не как художественное, а как физическое явление, то потребуются математические инструменты.
Звук – это волна, которая поддается описанию математическими и физическими формулами. Каждое значение определенной волны, ее характеристику можно описать только цифровым значением.
Звуки бывают различными по высоте. Высота – это одно из основных свойств музыкального звука. Она зависит от частоты колебаний звуковой волны. Частота (скорость) равняется числу колебаний в секунду и измеряется в герцах. Математически доказано: чем больше частота колебаний, тем выше звук.
Человеческое ухо воспринимает звуки, частота которых заключается в пределах от 16 Герц до 16 000 Герц. В музыке используется диапазон от 20 до 5 000 колебаний в секунду. Например:
ноте ля 1-ой октавы соответствует частота волны 440 Гц,
ноте ми 2-ой октавы соответствует частота волны 660 Гц,
ноте ля 2-ой октавы соответствует частота волны 880 Гц.
Система координат. Графическое изображение музыки.
Сходства можно увидеть в знакомом всем инструменте – фортепьяно. Расположение октав на этом инструменте можно сравнить с координатной прямой. Координатная прямая не имеет конца и начала, но имеет точку О (0), которая делит её на равные части, Справа от точки О находятся положительные числа по порядку (1, 2, 3…), а слева - отрицательные в обратном порядке (-1, -2, -3…). На клавиатуре фортепьяно примерно также: она условно делится на равные части. Справа от середины клавиатуры октавы идут по порядку (1-ая октава, 2-ая октава, 3-я октава …), а слева - в обратном порядке (малая, большая, контроктава, субконтроктава).
Сходства музыки и математики можно увидеть и в системе координат. Такая простая и привычная вещь, как система координат, была введена в математический инструментарий не так давно: ее изобрел Декарт в XVII веке. Сейчас трудно себе представить развитие алгебры и геометрии без системы координат. Но интересно, что математика лишь с XVII века пользуется этой замечательной системой. А в музыке примерно ту же систему координат стали использовать еще с XI века, когда систему записи музыки разработал Гвидо Аретинский.
Как математические модели являются отражением действительности, так и музыкальная нотация является графическим представлением физического явления. Музыка записывается на бумаге с помощью нотного стана, который можно считать графиком изменения высоты звуков с течением времени. Нотный стан можно представить как систему координат, на вертикальной оси которой обозначается высота звука, на горизонтальной – время, т.е. момент появления звуков.
Высокие ноты расположены на нотном стане выше, чем низкие. Звуки низкой частоты располагаются на нижних линиях нотного стана. Звуки, расположенные на одной линии нотного стана, имеют одинаковую высоту (частоту). Чем дальше по вертикали расположены друг от друга ноты на нотных линейках, тем больше расстояние (интервал) между ними. Последовательность звуков, высота которых непрерывно возрастает, называют восходящей. И наоборот, последовательность, у которой звуки убывают, называют нисходящей.
На нотных линиях по горизонтали изображают чередования длительностей звуков и пауз. Например, 3 звука, исполняемые последовательно один за другим, записываются по горизонтали (слева направо) друг за другом (как «гусеница»). Они звучат в разные моменты времени. Если эти же 3 звука исполняются одновременно, то они будут изображаться по вертикали один под другим (как «снеговичок»). То есть звуки, расположенные вертикально друг под другом, исполняются одновременно (в один и тот же момент времени).
Мелодии обычно сравнивают с рисунками из точек и линий. Движение мелодии во времени можно представить графически в виде кривой. Действительно, посмотрев на запись нот, мы увидим не что иное, как самый настоящий график музыки. Причем, разные мелодии будут выражаться в виде разных кривых. Мелодия может быть:
- монотонно-плавной (это можно представить в виде ровной горизонтальной прямой без скачков);
- волнообразной (как синусоидная кривая с небольшой амплитудой) ;
- скачкообразной с резкими перепадами в звуках (это может быть зигзагообразная, ломаная кривая с большими скачками);
- прерывистой с остановками - паузами (например, пунктирно-прерывистая линия);
- восходящей или нисходящей (движение по кривой вверх или вниз) и т.д.
Здесь можно говорить о геометрии композиции, геометрическом представлении мелодии. Все эти примеры показывают, что музыка и геометрия сливаются, между ними есть общее.
Длительности. Дроби.
Звук имеют свою длину – длительность. Длительность – это продолжительность звучания. В музыке различают: относительную и абсолютную длительность звуков.
Абсолютная длительность устанавливается темпом, т.е. скоростью звучания (быстро, медленно, умеренно) и - более точно - по прибору метроному.
Относительная длительность – продолжительность данного звука по сравнению с другими. В отношении длительности нот и пауз можно провести прямую параллель к математическому понятию целых чисел и дробей. Здесь и происходит сопоставление целого числа и целой длительности, дробного числа и дробной длительности. Длительности коротких нот выражаются через дробные числа, записываются при помощи дроби. Свои названия длительности музыкальных нот позаимствовали у дробей. Они возникают при делении целой на равные доли. Целая нота принята в музыке за единицу (1).
В музыке ноты и паузы бывают: целые (1), половинные (1/2), четвертные (1/4), восьмые (1/8), шестнадцатые (1/16), тридцать вторые (1/32)… Их связывает между собой математическая закономерность. Например, четвертная нота показывает, что она звучит по длительности в 4 раза быстрее, чем целая нота. В целой ноте содержится: 2 половинных нот, или 4 четвертных нот, или 8 восьмых нот… В половинной ноте содержится: 2 четвертных нот, или 4 восьмых нот, или 8 шестнадцатых нот…Это означает, что за время звучания целой ноты можно исполнить 2 половинных ноты, за время исполнения половинной ноты могут прозвучать 2 четвертные и т.д. Над музыкальными дробями можно производить такие же операции, как и с обычными дробями в математике, например, операции сложения, вычитания и др.
Примеры формул длительностей нот и разных вариантов их записи:
1 = 1/2 + 1/2 = 1/4+1/4+1/4+1/4 = 1/8+1/8+1/8+1/8+1/8+1/8+1/8+1/8 = 1/2+1/4+1/4
1/2 = 1/4+1/4 = 1/8+1/8+1/8+1/8 = 1/4+1/8+1/8 = 1/8+1/8+ 1/16+1/16+ 1/16+1/16
1/4 = 1/8+1/8 = 1/16+1/16+1/16+1/16 =1/8+1/16+1/16
Не зная математических понятий, не умея различать дроби, сравнивать их, совершать с ними математические операции, невозможно было бы читать ноты и сыграть правильно записанную мелодию.
Прогрессия.
В музыке принцип построения длительностей нот соответствует принципу построения геометрической прогрессии. По степени убывания запись длительностей нот выглядит так: 1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128. В математике это - бесконечная геометрическая прогрессия.
С арифметической прогрессией связано понятие в музыке «квинтовый круг тональностей», который определяет порядок расположения тональностей (по кругу через интервал в чистую квинту).
Ритм.
Ритмом называется чередование элементов, происходящее с определенной периодичностью. В математике ритм – это чередование чисел. Исследуя математические закономерности и числовые последовательности, в них часто можно обнаружить ритмичность. Например, дробь 2/82 можно записать как в виде бесконечной периодической дроби: 2/82=0, 0243902439…=0, (02439).
Ритм в музыке – частота, с которой воспроизводится последовательность звуков. Ритм – важный элемент в музыке, это яркое выразительное средство. Говорят, что «душа» музыки – это ритм. Мелодия образуется только в том случае, если звуки организованы ритмически. Чередование звуков вне определенного ритма не воспринимается как мелодия. Ритм определяет характер произведения. Благодаря ему, мы можем определить жанр звучащей музыки: марш, вальс, мазурка или полька. У каждого музыкального произведения есть свой ритмический рисунок – последовательность длительностей, часто повторяющаяся в произведении.
Еще ритм может выражаться в периодическом повторении частей музыкального произведения. Например, в песне несколько раз повторяются куплет и припев, или в форме «рондо» равномерно чередуются и повторяются определенные эпизоды.
Некоторые считают, что слово «ритм» изначально принадлежало музыке, а математика заимствовала данное слово.
Темп, скорость.
Темп в музыке используется также, как и в математике. Темп (скорость) – это отношение числа происходящих событий, движения к тому времени, которое они заняли. Под музыкальным темпом понимают скорость исполнения произведения, быстроту звучания. В музыке различают множество оттенков по темпу звучания (они обозначаются итальянскими терминами), например:
анданте – не спеша, умеренно,
адажио – медленнее, чем анданте,
андантино – чуть живее, чем анданте,
аллегро – весело, живо, быстро,
ленто – медленно,
лярго – очень медленно,
ляргетто – подвижнее, чем лярго,
престо – очень быстро, скоро,
престиссимо – исключительно быстро, быстрее, чем престо,
виво – быстро, живо.
Как видно, нужно иметь опыт, чутье, слух, чтобы различать все оттенки музыкальных темпов. Отклонение от заданного темпа ведет к искажению произведения. Точное определение темпа дают показатели по метроному – прибору, который помогает установить правильную скорость исполнения. Темп – важное условие выразительного исполнения музыки.
Параллельность.
В музыке, как и в математике, есть понятие параллельности. В музыке есть параллельные тональности – это такие тональности в мажоре и в миноре, которые имеют одинаковый звуковой состав (и одинаковые знаки при ключе), но строятся от разной тоники (начальной ступени гаммы). Тоники параллельных тональностей всегда отстоят друг от друга на определенный интервал (на малую терцию). Примерами параллельных тональностей являются: до мажор и ля минор, ми-бемоль мажор и до минор, соль мажор и ми минор.
Параллельность можно заметить и при транспонировании звуков. Транспонирование – перемещение звуков музыкального произведения на один и тот же интервал вверх или вниз. Это применяется для удобства исполнения.
Если два голоса одновременно исполняют одну и ту же мелодию, но один – в верхнем регистре, а второй – в нижнем, то это называется параллельным звучанием голосов. Параллельно могут звучать голос и инструмент, сопровождающий его (например, со сдвигом на октаву).
А еще линии нотного стана всегда параллельны, никогда не пересекаются. Музыканта интересует не только, что одна нота выше другой, а на сколько. Разницу в высоте помогают измерить параллельные линейки нотного стана. Например, расстояние между двумя соседними 1-ой и 3-ей линиями равно 3-м ступеням, между 1-ой и 3-ей линиями – 5-ти ступеням, между 1-ой и 5-ой линиями – 7-ми ступеням.
Параллельны и струны некоторых музыкальных инструментов: гитары, арфы, домры, балалайки, скрипки, виолончели, контрабаса, гуслей и др.
Счет.
В музыке арифметический счет присутствует во многом. К примеру, приходится просчитывать ритм, паузы (чтобы вовремя вступить), длительности, счет используется, чтобы совмещать ноты различной длительности, определять параллельные тональности, строить интервалы и аккорды, переходить со скрипичного ключа на басовый, транспонировать мелодию и во многом другом, где требуется арифметика.
Наличие противоположностей.
И в музыке, и в математике используется такие понятия, как противоположности.
Примеры противоположных понятий в математике :
больше – меньше, сложение – вычитание, умножение – деление, четное – нечетное, простое – составное, отрицательное – положительное, прямая – кривая, плюс – минус, одночлен – многочлен.
Примеры противоположных понятий в музыке:
повышение – понижение, мажор – минор, быстро – медленно, громко – тихо, высокий – низкий, длинный – короткий, одноголосие – многоголосие.
Сравнительный анализ этих примеров показывает наличие одинаковых, т.е. общих понятий и в музыке, и в математике.
Симметричность.
Принцип симметрии, использующийся в математике (особенно, в геометрии), встречается и в музыке. Симметрия наблюдается не только в музыкальных тактах, фразах и мотивах. В более крупных музыкальных структурах композиторы используют свойство симметричности. Сущность симметрии – в правильном периодическом повторении частей. Ряд музыкальных произведений строится симметрично.
Есть композиции, обладающие простой симметрией, где полностью повторяется единственный фрагмент (А). Его схема выглядит так: А-А-А…
Произведение, состоящее из 2-х полностью различных групп, напротив не обладает какой-либо симметрией. Его схема: А-В.
Есть произведения, обладающие более широкой симметрией. В них части композиции могут повторяться, образуя различные симметричные структуры. Например: А-В-А; А-В-А-В-А; А-В-С-Д-С-В-А.
Также существуют сложные формы, состоящие из нескольких частей, каждая из которых также делится на части с симметрией внутри. Пример сложных структурных симметрий: А (а-б-а) – В ( с-д-с) – А (а-б-а).
«Золотое сечение».
Принцип «золотого сечения» в математике заключается в пропорциональном делении отрезка на неравные части, при котором весь отрезок так относится к большей части, как большая часть относится к меньшей части (или меньший отрезок так относится к большему, как больший ко всему). Математически это выражается так:
а : в = в : с ( или с : в = в : а),
где с = а + в ,
с - весь отрезок, состоящий из 2-х неравных отрезков,
а - меньший отрезок,
в – больший отрезок.
«Золотое сечение» пронизывает всю историю искусства. Например, пирамиды Хеопса, знаменитый греческий храм Парфенон, большинство греческих скульптурных памятников, картины Рафаэля, Леонардо да Винчи. Эти выдающиеся произведения искусства наполнены гармонией, основанной на «золотом сечении». Используется оно и в музыке.
Исследователи открыли и в музыке «золотую пропорцию», которая определяет точное место кульминации произведения. «Золотое сечение» встречается в большинстве классических сочинений у выдающихся композиторов: Баха, Моцарта, Шопена, Шуберта, Скрябина, Аренского. Эти произведения разделены своей высшей точкой, моментом максимального напряжения на части (или по теме, или по интонации, или по ладу), которые находятся между собой в отношении «золотой пропорции». Кульминация этих сочинений располагается в точке деления «золотого сечения». Кульминация – взлет, высшая точка в музыкальном произведении, в котором сначала наблюдается длительный период нарастания эмоционального напряжения, затем «остановка» и после более краткий период спада.
У гениальных композиторов (особенно, у Баха) наблюдается наибольшее число произведений, где встречается «золотое сечение». Вероятно, композиторы получили этот результат интуитивно, стремясь придать своей музыке равновесие. А математики доказали присутствие принципа «золотого сечения» в их сочинениях. Творчество состоит в поиске формы: композитор объединяет большое и малое, сочетает напряженные и смягченные моменты, прямые и кривые, высокие и низкие звуки. В результате достигается некое стабильное или нестабильное равновесие. Оценка результата творчества зрителем может быть субъективной. Объективным критерием красоты является «золотое сечение». Пропорциям «золотого сечения» подчинены все гармонические формы, оно является критерием гармонии.
Мыслительные способности.
Музыка расширяет и усиливает возможности человека: душевные, интеллектуальные и другие. Существует большое число выдающихся и просто успешных людей, которые не стали музыкантами, но любят музыку и музицируют. Среди них: короли и президенты, политики и бизнесмены, художники и артисты. Музыка многогранна и требовательна ко всем человеческим качествам. Музыкант должен быть: дисциплинированным, четким, мыслящим, волевым, сосредоточенным, внимательным, памятливым, чутким, обладающим координацией. Многие выдающиеся музыканты блистали математическими способностями. Например:
- Эрнест Ансерли - профессиональный математик и лучший исполнитель Стравинского;
- Леонид Сабанеев – выпускник математического факультета Московского университета, прекрасный пианист, композитор, друг Скрябина;
- композитор Эдисон Денисов преподавал математику в Томском университете;
- виолончелист К.Давыдов закончил физико-математический факультет.
Это говорит о близости музыкальных и математических способностей. Эти и другие примеры показывают, что математика дружит с музыкой, иногда они идут рядом, пересекаясь.
Музыка позволяет раскрыть способности человека. Она стимулирует работу мозга. Занимаясь ей, можно развить математические навыки.
Заключение
В своей работе я постаралась показать связь математики и музыки. Данные исследования доказывают, что математика и музыка имеют общие точки соприкосновения, общие свойства. Моя работа дает более широкое представление о присутствии и использовании математики в музыке.
Математика, как наука, может развиваться без музыки. Но музыкальное искусство во многом подчиняется законам математики. Математика помогает изучать музыку. Математика пересекает музыку, пронизывает ее.
Для выявления связи математики и музыки я изучила и проанализировала много литературы, ознакомилась с историей формирования теории музыки у Пифагора. Композиторы сочиняли музыку, может быть не зная математики. Но для записи им требовалась нотная запись, которая математична. Музыка пропитана математикой. Многие музыканты-композиторы не подозревали о «математической красоте» своих произведений, у них отмечается сильная интуиция формы и стройности.
Список используемой литературы