Накарякова Евгения Андреевна, 4 "А" класс, МАОУ Гимназия №13, г. Екатеринбург, Свердловская область, Россия
Научный руководитель: Дорожкина Вероника Петровна, учитель математики, МАОУ Гимназия №13, г. Екатеринбург, Свердловская область, Россия
«Удивительное число – ноль»
«Удивительное число – ноль»
1. ВВЕДЕНИЕ
Моя проектная работа называется «Удивительное число – ноль». Это краткосрочный проект, объединяющий такие области знаний как математика, литература.
Цель проекта: узнать историю появления нуля, показать значимость открытия этой цифры.
Задачи:
- изучить историю возникновения числа 0:
- изучить специфические свойства числа 0;
- выяснить применение числа 0 в других областях знаний, кроме математики;
- выяснить какое значение число 0 имеет в практической жизни людей;
- выяснить место нуля в литературном и народном творчестве.
Актуальность:
Люди всегда используют числа и цифры везде: в работе, в быту, на отдыхе. Математика играет важную роль в естественнонаучных, инженерно-технических и гуманитарных исследованиях. Без современной математики был бы невозможен прогресс в различных областях человеческой деятельности.
Методы исследования: поиск и сбор информации из различных источников (научно-популярной литературы, сайтов сети Интернет), обобщение и анализ полученных данных.
Объект исследования: удивительное число – НОЛЬ.
Продуктом проекта стала презентация, содержащая: историю числа ноль, специфические свойства числа 0, значение число 0 в практической жизни людей, место нуля в литературном и народном творчестве.
Практическая значимость: возможность использования полученной информации на уроках и внеурочное время по математике, применение в повседневной жизни.
Первое, что нужно сказать о нуле, это то, что имеется два варианта его использования, оба очень важные, но немного различные. Один путь – это указатель пустого разряда в нашей позиционной системе счисления. Так, в числе 2307 нуль служит для того, чтобы позиции 2 и 3 были верными. Очевидно, что 237 значит совершенно иное. Второй вариант использования нуля – это число, которое мы обозначаем 0.
История обоих вариантов была сложной.
От латинского nullis ("никакой") произошло слово, обозначающее одно из важнейших математических понятий. Оно включает не только символ – цифру, помогающую вести счет, записывать математические операции. Это целая концепция. Отсутствие какого-либо количества, пустота, начало и бесконечность - философское отношение к этим понятиям было различным в разные эпохи и в разных странах.
Потребность в подсчёте стала очевидной для человека с самого начала формирования первобытного общества. Свои числовые системы, со специфическими цифровыми обозначениями, формировались во всех обособленных центрах цивилизации: в Египте и Древнем Вавилоне, в Китае и Индии, у южноамериканских индейцев и в античной Греции. Математика прошла путь от простейшего подсчета предметов до решения сложнейших современных задач. При этом история числа ноль насчитывает только небольшую часть этого срока.
История числа ноль – это процесс возникновения математического понятия и начало применения символа, его обозначающего. Символ, обозначающий его, впервые появился у математиков и астрономов на глиняных клинописных табличках Древнего Вавилона.
Цифра ноль, или знак, принятый вавилонянами для обозначения разряда, выглядели как два поставленных под углом клинышка или стрелы. Этот символ был составной частью числа и не участвовал в арифметических действиях – складывать или умножать на него было нельзя.
Например, вавилоняне, не зная о нуле, вполне отличали числа 202 от 22. В пустующую ячейку записывались два клинышка, обозначавшие пустоту. Это делали еще около 300 года до нашей эры.
Независимо от математиков Месопотамии свой ноль ввели в обиход индейцы Центральной Америки - майя и инки (древние майя обозначали ноль стилизованным изображением ракушки). Общим для обеих систем счисления было то, что они не развивали идею нуля как числа. Древнеамериканская цивилизация оставила миру множество достижений в интеллектуальной сфере. Сложные календарные системы майя и инков – результат многовекового опыта астрономических наблюдений и сложнейших математических расчетов. Но ноль у майа означал не ноль в нашем понимании слова, а "начало". Счет дней в календаре майя начинался с нулевого дня и назывался Ахау.
Соседи Инки использовали узелковое письмо, где цифры от 1 до 9 обозначались разными узелками, а ноль — пустым местом. Но никогда в их уравнениях цифра ноль не присутствовала в качестве числа, влияющего на результат математических операций.
Римляне о нуле не знали. Если записать число 388 римскими цифрами получится CCCLXXXVIII. Никакого понятия о разрядах.
Система десятичных разрядов существовала и в Китае. Чтобы записать число 934 в столбик единиц клали 4 палочки, десятков — 3, а сотен — 9 палочек. Вместо нуля оставляли пустое место. А вот записывая цифры китайцы разряды не использовал и символа для ноля не было.
Главным наследием древнегреческих математиков были их достижения в геометрии и астрономии. Числа в их представлении - это отрезки, имеющие начало, конец и определенную длину. Ноль — это число, не имеющее в этом случае практической ценности. Отрезок с нулевой длиной в античной математике и философии не имел смысла. Одним из главных постулатов учения Аристотеля является фраза Natura abhorret vacuum – "Природа не терпит пустоты". Бесконечность, ничто, несуществование – эти категории не вписывались в античное мироздание. Поэтому современный смысл вопроса "каким числом является 0" был недостижим для Архимеда, Пифагора или Евклида, хотя похожий на ноль символ встречается в таблицах великого астронома Птолемея. Букву "Омикрон" (первая буква в слове οὐδέν – "ничего") он проставлял в пустых клетках.
Теперь перенесемся в Индию, где, как справедливо было бы сказать, родилась система цифр и чисел, которая превратилась затем в достаточно сложную, ту, которую мы используем сегодня.
Не вызывает сомнения, что использование нуля как числа пришло в индийскую математику около 650 г. н.э.
Что же изобрели индийские математики? Махавира (850 г.), Брахмагупта (1114 г.), Ариабхата (476 г.) - авторы трактатов, в которых во многом оформилась современная система записи чисел и правила основных арифметических операций. Они записали ноль по началу точкой, обозначая отсутствующее число, потом и кружочком. Но главное, что они определили ноль не как понятие отсутствия числа, а как число.
- Около 500 года нашей эры была разработана позиционная система записи чисел, а запись, касающаяся использования нуля, датируется 876 годом. Индийские математики Брахмагупта, Махавира и Бхаскара писали, что если из одного числа вычесть его же, то получится ноль. Это и есть знакомое нам определения числа ноль. Теперь ноль — это число. Ноль используется в расчетах и даже записывается как маленький кружочек. Всего 10 цифрами можно записать любое даже самое большое число. Это была революция в математике. Индийцы называли ноль "сунья", пустой. Арабы перевели это как "сыфр", от которого произошло слово "цифры". Кстати, индийские же математики, разделив на нуль, получили бесконечность.
Историки считают, что десятичность системы счисления была заимствована индийцами у китайцев, а позиционный характер её – у вавилонян.
Блестящие работы математиков из Индии распространились на запад, в арабские и исламские страны. Сначала они попали к Аль-Хорезми, который написал книгу об индийском искусстве вычислений, которая описывает индийскую позиционную систему счисления, основанную на цифрах от 1 до 9 и 0. Эта работа была первой в странах, где находится сейчас Ирак, в которой нуль использовался на месте отсутствующего разряда.
Индийские идеи распространились на восток, в Китай, как и в мусульманские страны.
Фибоначчи был одним из тех, кто сыграл важную роль в том, чтобы принести новые идеи о системах счисления в Европу:
“Важным связующим звеном между индийско-арабской системой счисления и европейскими математиками является Фибоначчи, итальянский математик”.
Примерно в 1200 г. в работе Книга абака (Liber Abaci) он описал девять индийских символов вместе со знаком нуль для европейцев, но этот труд долгое время широко не использовался.
К 1600 годам нуль начал широко применяться, но только после сильного сопротивления.
В России ноль вводился в практику стараниями Леонтия Магницкого, автора знаменитого учебника «Арифметика, сиречь наука числительная» (1703).
Нуль - это четное, не имеющее знака натуральное целое число. Сложение с нулем и вычитание нуля никак не влияет на число, а умножение на 0 даёт ноль.
Ноль является чётным числом, поскольку при делении его на 2 получается целое число:
{\displaystyle 0/2=0}0/2=0
Число 0 в обычных арифметических операциях ведет себя совершенно уникально:
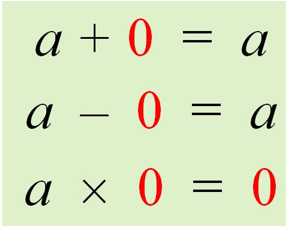
2. Число 0 – это единственное число, на которое нельзя делить.
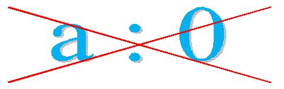
Число 0 – это единственное действительное число, которое не является ни положительным, ни отрицательным.
Ноль, который разграничивает положительные и отрицательные числа, обладает уникальными математическими свойствами. Деление на ноль считается не имеющей смысла операцией, которое в случае выполнения в компьютерной программе может нанести системе существенный вред. Именно в попытке деления на 0 оказался смысл сбоя в компьютерной системе крейсера ВМФ США "Йорктаун", который произошел осенью 1997 года и привел к несанкционированному выключению двигательной установки. Некорректное отношение к числу, означающему "ничто", превратило мощный военный корабль в беспомощную неподвижную цель.
Значение этого числа существенно возрастало с развитием науки. Нуль возникает в областях не только чисто математических. Ноль часто используется как начало отсчёта. Примеры весьма многочисленны.
Бинарное счисление, послужившее основой для создания современных вычислительных устройств, является позиционной системой счисления с основанием два. Это означает, что все данные, вводимые в компьютерные системы, кодируются сочетанием двух символов – единицы и нуля. Роль компьютеров в современном мире становится определяющей для всех сторон жизни, а значит, история числа ноль, без которого их появление было бы невозможно, продолжается.
- В центре города Будапешт (Венгрия) находится памятник НУЛЮ.
В 1849 году в Будапеште возведён Цепной мост, где установили нулевой километр – точку отсчёта расстояний в Венгрии. От этого памятника отмеряются все расстояния в стране.
Нуль – это единственная цифра, которой поставлен памятник.
- На любом калькуляторе после его включения сразу появляется ЕДИНСТВЕННОЕ число – цифра 0.
- В полночь на электронных часах появляются четыре НУЛЯ. Начинается новый день!
- КРЕСТИКИ-НОЛИКИ – логическая игра, в которой один из игроков играет “крестиками”, а второй — “ноликами”.
- Жест рукой, изображающий цифру 0, в англоговорящих странах имеет значение “ВСЕ В ПОРЯДКЕ”, “ВСЕ НОРМАЛЬНО”, “ВСЕ ОТЛИЧНО”.
- Число 0 имеет два названия: НУЛЬ и НОЛЬ.
Оба названия в свободном употреблении – равноправны.
В терминологическом значении (особенно в косвенных падежах) обычно используется вторая, например: равняется нулю, температура держится на нуле. Производное прилагательное обычно образуется от формы нуль, например: нулевой меридиан, нулевая отметка.
«Мы почитаем всех нулями, а единицами — себя» — цитата из поэмы Пушкина «Евгений Онегин»[12] (глава 2, строфа 14), употребляется иронически, когда говорят о чьем-либо завышенном самомнении и пренебрежительном отношении к окружающим[13].
На нуле — отсутствие чего-либо. Например, «финансы на нуле» (разговорное употребление)[14].
Ноль в переносном значении означает ничтожного, незначительного человека, например: «Он абсолютный ноль»[14].
Выражение ноль без палочки, когда идёт речь о человеке, означает, что он не имеет никакого влияния, значения (разговорное и шутливое употребление)[14], а также некомпетентного, глупого человека[15].
Ноль внимания — отсутствие внимания[14].
Выражение ноль-ноль, употребляемое после указания часа суток, означает: ровно в таком-то часу, без минут[14]. В спорте это же выражение может обозначать ничейный исход игры, состязания[16].
С нуля начинать — начинать на пустом месте (разговорное употребление)[14] или приступать к чему-либо без предварительной подготовки[16].
Стричь под ноль — то же, что стричь наголо[1
Следующее свойство числа 0 очень хорошо иллюстрируется известным стихотворением Самуила Яковлевича Маршака.
Вот это ноль иль ничего.
Послyшай сказкy про него.
Сказал веселый, крyглый ноль
Соседке - единице:
- С тобою рядышком позволь
Стоять мне на странице!
Она окинyла его
Сердитым, гордым взглядом:
- Ты, ноль, не стоишь ничего.
Не стой со мною рядом!
Ответил ноль: - Я признаю,
Что ничего не стою,
Но можешь стать ты десятью,
Коль бyдy я с тобою.
Так одинока ты сейчас,
Мала и хyдощава,
Но бyдешь больше в десять раз,
Когда я бyдy справа.
Напрасно дyмают, что ноль
Играет маленькyю роль.
Мы двойкy в двадцать превратим.
Из троек и четверок
Мы можем, если захотим,
Составить тридцать, сорок.
Пyсть говорят, что мы ничто, -
С двyмя нолями вместе
Из единицы выйдет сто,
Из двойки - целых двести!
Когда-то многие считали,
Что нуль не значит ничего.
И, как не странно, полагали,
Что нуль совсем не есть число.
Но на оси средь прочих чисел,
И все действительные числа
На два разряда разделить.
Нуль ни в один из них не входит -
Он сам составил чисел класс.
О всех его особых свойствах
Мы поведём сейчас рассказ.
Коль нуль к числу ты прибавляешь,
Иль отнимаешь от него,
В ответе тотчас получаешь
Опять то самое число.
Попав как множитель средь чисел,
Он сводит мигом всех на нет.
И потому в произведенье
Один за всех несёт ответ.
А относительно деленья,
Во-первых, нужно помнить то,
Что уж давно в научном мире
Делить на нуль запрещено.
Причина всем вам очевидна.
А состоит причина в том,
Что смысла нет в таком деленьи,
Противоречье в нём самом.
И впрямь: какое из известных
Число за частное нам взять,
Когда с нулём в произведенье
Все числа нуль лишь могут дать?
"А" в нулевой есть единица -
Так все условились считать.
Но глубоко бы тот ошибся,
Кто б это вздумал доказать.
- Цифры все хоть что-то значат,
Только Ноль несчастный плачет –
Он не значит ничего,
Будто бы и нет его.
Девять с ним дружить не хочет,
Восемь голову морочит,
Семь, Шесть, Пять смеются вслед,
И Четверке дела нет.
Стали Три и Два дразниться.
И пошел Ноль к Единице.
Позади нее он встал
И ничем быть перестал.
Мне интересно было работать над этой темой. В процессе работы я много узнала интересного. Я теперь знаю историю возникновения числа нуль, некоторые свойства нуля, где можно применить число 0 в других областях знаний, кроме математики, какое значение число 0 имеет в практической жизни людей, место нуля в литературном и народном творчестве.
Теперь я смогу рассказать историю появления нуля одноклассникам, показать значимость открытия этой цифры.
1. Интернет ресурс: https://ru.wikipedia.org
2. Депман И.Я. “Из истории математики” – М : Детгиз, 1950. – 114 с.
3. Математика в школе : науч.-метод. журн – 1989. – №4.
4. Панишева О.В. Математика в стихах. 5-11 классы: задачи, сказки, рифмованные правила – Волгоград : Учитель, 2009. – 219 с.
5. Интернет ресурс: https://luktore.to
6. Интернет ресурс: https://otvet.mail.ru
